题目内容

计算（2
7
9
）0.5+0.1-2+（2
10
27
） 
2
3
-3π0+
37
48
=
 
．
考点：有理数指数幂的化简求值
专题：函数的性质及应用
分析：本题考查了指数幂的运算法则，属于基础题．
解答： 解：原式=(
5
3
)2×0.5+10-1×（-2）+(
4
3
)3×
2
3
-3+
37
48

=
5
3
+100+
16
9
-3+
37
48

=102
109
144
．
故答案为：102
109
144
．
点评：本题考查了指数幂的运算法则，属于基础题．
练习册系列答案
相关题目
在锐角△ABC中，角A、B、C的对边分别为a、b、c，若b=4，且（a2+c2-b2）tanB=
3
ac，则△ABC面积的最大值是
 
．
甲乙两人下棋，甲胜乙的概率为0.4，甲不输的概率为0.9，则甲、乙和棋的概率是
 
．
设A={y|y=-1+x-2x2}，若m∈A，则必有（　　）
A、m∈{正有理数}
B、m∈{负有理数}
C、m∈{正实数}
D、m∈{负实数}
已知向量
m
=（sinωx，cosωx），
n
=（cosωx，cosωx），其中ω＞0，函数f（x）=2
m
•
n
-1的最小正周期为π．
（Ⅰ） 求ω的值；
（Ⅱ） 求函数f（x）在[
π
6
，
π
4
]上的最大值．
设各项均不为0的数列{an}满足an+1=
2
an（n≥1），Sn是其前n项和，若a2a4=2a5，则S4=（　　）
A、4
2
B、8
2
C、3+3
2
D、6+6
2
已知集合A={x∈Z|x2-1≤0}，B={x|x2-x-2=0}，则A∩B=（　　）
A、∅B、{-1}
C、{0}D、{2}
用“＜”或“＞”号填空：0.30.8
 
0.30.7．
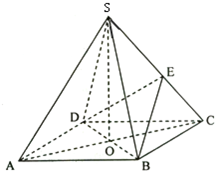已知如图，在四棱锥S-ABCD中，底面ABCD是菱形，AC与BD的交点为O，SO⊥平面ABCD，E为侧棱SC上一个动点．
（1）求证：平面SAC⊥平面BDE；
（2）若E为SC的中点，求证：SA∥平面BDE；
（3）若E为SC的中点，AB=SO=a，∠BAD=60°，求三棱锥S-BDE的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网