题目内容
已知f(x)是定义在R上的函数,给出下列四个命题:
①若f(x)是奇函数,则f(x)•f(-x)≥0;
②若f(x)是偶函数,则f(x)•f(-x)≥0;
③若f(x)是增函数,则f(x)≥f(-x);
④若f(x)是增函数,则f(|x|)≥f(x).
其中正确的是 .(将你认为正确的命题的序号都填上).
①若f(x)是奇函数,则f(x)•f(-x)≥0;
②若f(x)是偶函数,则f(x)•f(-x)≥0;
③若f(x)是增函数,则f(x)≥f(-x);
④若f(x)是增函数,则f(|x|)≥f(x).
其中正确的是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,利用奇函数的定义,f(x)是奇函数,则f(-x)=-f(x),易判断f(x)•f(-x)≤0,可判断①;
②,利用偶函数的定义,f(x)是偶函数,则f(-x)=f(x),易知f(x)•f(-x)≥0,可判断②;
③,若f(x)是增函数,则当x<0时,-x>0,易知f(-x)≥f(x),可判断③;
④,利用|x|≥x,f(x)是增函数,可知f(|x|)≥f(x),可判断④.
②,利用偶函数的定义,f(x)是偶函数,则f(-x)=f(x),易知f(x)•f(-x)≥0,可判断②;
③,若f(x)是增函数,则当x<0时,-x>0,易知f(-x)≥f(x),可判断③;
④,利用|x|≥x,f(x)是增函数,可知f(|x|)≥f(x),可判断④.
解答:
解:对于①,若f(x)是奇函数,则f(-x)=-f(x),f(x)•f(-x)=-f2(x)≤0,故①错误;
对于②,若f(x)是偶函数,则f(-x)=f(x),f(x)•f(-x)=f2(x)≥0,故②正确;
对于③,若f(x)是增函数,则当x<0时,-x>0,f(-x)≥f(x),故③错误;
对于④,若f(x)是增函数,由于|x|≥x,故f(|x|)≥f(x),故④正确.
综上所述,正确的是:②④,
故答案为:②④.
对于②,若f(x)是偶函数,则f(-x)=f(x),f(x)•f(-x)=f2(x)≥0,故②正确;
对于③,若f(x)是增函数,则当x<0时,-x>0,f(-x)≥f(x),故③错误;
对于④,若f(x)是增函数,由于|x|≥x,故f(|x|)≥f(x),故④正确.
综上所述,正确的是:②④,
故答案为:②④.
点评:本题考查命题的真假判断与应用,着重考查函数的奇偶性、单调性的理解与应用,熟练地应用奇偶函数的概念及单调性的定义进行分析判断是关键,属于中档题.

练习册系列答案
相关题目
函数f(x)=
+
的定义域是( )
| x+3 |
| (2x+3)0 | ||
|
A、[-3,
| ||||||
B、[-3,-
| ||||||
C、[-3,
| ||||||
D、[-3,-
|
已知集合M={x|x≤1},P={x|x>t},若M∩P≠∅,则实数t应该满足的条件是( )
| A、t>1 | B、t≥1 |
| C、t<1 | D、t≤1 |
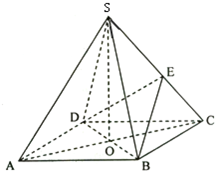 已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.
已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.