题目内容
已知函数f(x)=x+
.
(1)证明:f(x)在[1,+∞)上是增函数;
(2)求f(x)在[2,4]上的最值.
| 1 |
| x |
(1)证明:f(x)在[1,+∞)上是增函数;
(2)求f(x)在[2,4]上的最值.
考点:函数单调性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用定义证明单调性步骤:①取值、②作差、③变形、④判号、⑤下结论,进行证明;
(2)利用f(x)的单调性求出函数在已知区间上的最值.
(2)利用f(x)的单调性求出函数在已知区间上的最值.
解答:
(1)证明:设x1,x2∈[1,+∞),且x1<x2,
则f(x1)-f(x2)=x1+
-(x2+
)=x1-x2+
=
,
∵1≤x1<x2,∴x1-x2<0,x1x2>1,
∴x1x2-1>0,则
<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
所以y=f(x)在[1,+∞)上是增函数;
(2)解:由(1)知,函数f(x)在[2,4]上是增函数,
当x=2时,f(x)有最小值是f(2)=
,
当x=4时,f(x)有最大值是f(4)=
,
所以函数的最小值为
,最大值为
.
则f(x1)-f(x2)=x1+
| 1 |
| x1 |
| 1 |
| x2 |
| x2-x1 |
| x1x2 |
=
| (x1-x2)(x1x2-1) |
| x1x2 |
∵1≤x1<x2,∴x1-x2<0,x1x2>1,
∴x1x2-1>0,则
| (x1-x2)(x1x2-1) |
| x1x2 |
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
所以y=f(x)在[1,+∞)上是增函数;
(2)解:由(1)知,函数f(x)在[2,4]上是增函数,
当x=2时,f(x)有最小值是f(2)=
| 5 |
| 2 |
当x=4时,f(x)有最大值是f(4)=
| 17 |
| 4 |
所以函数的最小值为
| 5 |
| 2 |
| 17 |
| 4 |
点评:本题考查了证明函数单调性的一种基本方法:定义法,以及利用函数的单调性求函数的最值,要熟练掌握定义证明单调性的步骤,其中变形最关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
设各项均不为0的数列{an}满足an+1=
an(n≥1),Sn是其前n项和,若a2a4=2a5,则S4=( )
| 2 |
A、4
| ||
B、8
| ||
C、3+3
| ||
D、6+6
|
设集合M={1,2,3}的非空真子集个数是( )
| A、6 | B、7 | C、8 | D、9 |
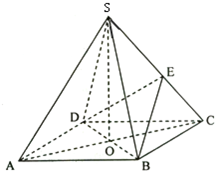 已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点.
已知如图,在四棱锥S-ABCD中,底面ABCD是菱形,AC与BD的交点为O,SO⊥平面ABCD,E为侧棱SC上一个动点. 如图,已知向量
如图,已知向量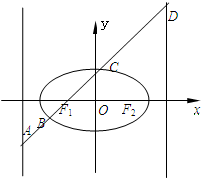 如图,已知椭圆
如图,已知椭圆