题目内容
△ABC中，|BC|=24，AC，BA边上的两条中线之和为39．若以BC边为x轴，BC中点为坐标原点建立平面直角坐标系．求：△ABC重心的轨迹方程．
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：设出三角形的重心G的坐标，由重心的性质结合AC，BA边上的两条中线之和为39得到|BG|+|CG|=26=2a，由此得到重心G的轨迹为椭圆并求得长半轴，再由|BC|=24得到半焦距，结合隐含条件求得b，则答案可求．
解答：
解：设重心为G（x，y），AC、AB边上的中线长之和等于39，
∴|BG|+|CG|=26=2a，a=13，
2c=|BC|=24，c=12，
∴b2=25，
∴重心G的轨迹方程是
+
=1（y≠0）．
∴|BG|+|CG|=26=2a，a=13，
2c=|BC|=24，c=12，
∴b2=25，
∴重心G的轨迹方程是
| x2 |
| 169 |
| y2 |
| 25 |
点评：本题考查了椭圆的定义与方差的求法，关键是对三角形重心性质的应用，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=x（x2-1）的图象大致是（ ）
A、 |
B、 |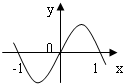
C、 |
D、 |
下列说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
| C、命题“a、b都是有理数”的否定是“a、b都不是有理数” |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
若随机变量ξ～N（100，σ2），且P（ξ≤120）=a，则P（ξ≥80）=（ ）
| A、a | ||
| B、1-a | ||
C、
| ||
D、
|
设{an}是任意等比数列，它的前n项和，前2n项和与前3n项分别为X，Y，Z，则下列等式中恒成立的是（ ）
| A、X+Z=2Y |
| B、Y（Y-X）=Z（Z-X） |
| C、Y2=XZ |
| D、Y（Y-X）=X（Z-X） |