题目内容
函数f（x）=x（x2-1）的图象大致是（ ）
A、 |
B、 |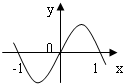
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：通过对函数的奇偶性进行研究，发现函数为奇函数，再考虑一些特殊值的取值，比如当0＜x＜1时，f（x）＜0，即可判断得到答案．
解答：
解：∵函数f（x）=x（x2-1），
则f（-x）=-x（x2-1）=-f（x），
故函数f（x）为奇函数，函数的图象关于原点对称，排除A、C，只能在B或D中选，
又当0＜x＜1时，x2-1＜0，∴f（x）＜0，只有D符合．
故选：D．
则f（-x）=-x（x2-1）=-f（x），
故函数f（x）为奇函数，函数的图象关于原点对称，排除A、C，只能在B或D中选，
又当0＜x＜1时，x2-1＜0，∴f（x）＜0，只有D符合．
故选：D．
点评：本题考查了函数的图象．研究函数图象一般从定义域、值域、单调性、对称性、恒过的定点等方面进行研究．同时，采用排除法解选择题是行之有效的方法．
练习册系列答案
相关题目
设A={x|y=
}，B={x|y=ln（1+x）}，则A∩B=（ ）
| 1-x |
| A、{x|x＞-1} |
| B、{x|x≤1} |
| C、{x|-1＜x≤1} |
| D、∅ |