题目内容
8.已知函数f(x)=x2,g(x)=-1nx,g'(x)为g(x)的导函数.若存在直线l同为函数f(x)与g'(x)的切线,则直线l的斜率为( )| A. | $2\sqrt{5}-4$ | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
分析 分别设出直线l与两个函数所对应曲线的切点,求出切线方程,由两切线系数相等列式求出切点横坐标,则答案可求.
解答 解:由g(x)=-1nx,得g'(x)=-$\frac{1}{x}$,
设直线l与f(x)的切点为(${x}_{1},{{x}_{1}}^{2}$),则f′(x1)=2x1,
∴直线l的方程为y-${{x}_{1}}^{2}=2{x}_{1}(x-{x}_{1})$,即$y=2{x}_{1}x-{{x}_{1}}^{2}$;
再设l与g'(x)的切点为(${x}_{2},-\frac{1}{{x}_{2}}$),则$g″({x}_{2})=\frac{1}{{{x}_{2}}^{2}}$,
∴直线l的方程为$y+\frac{1}{{x}_{2}}=\frac{1}{{{x}_{2}}^{2}}(x-{x}_{2})$,即$y=\frac{1}{{{x}_{2}}^{2}}x-\frac{2}{{x}_{2}}$.
∴$\left\{\begin{array}{l}{2{x}_{1}=\frac{1}{{{x}_{2}}^{2}}}\\{{{x}_{1}}^{2}=\frac{2}{{x}_{2}}}\end{array}\right.$,解得x1=2.
∴直线l的斜率为2x1=4.
故选:C.
点评 本题考查利用导数研究过去线上某点处的切线方程,函数在曲线上某点处的导数,就是函数在该点处的导数值,是中档题.

练习册系列答案
相关题目
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
| A. | $\frac{2}{3}$钱 | B. | $\frac{5}{6}$钱 | C. | 1钱 | D. | $\frac{7}{6}$钱 |
3.已知函数f(x)=1n(x+2)+1n(x-2),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
13.设集合A={x|x>2},B={x|x2-4x<0},则A∩B=( )
| A. | (4,+∞) | B. | (2,4) | C. | (0,4) | D. | (0,2) |
20.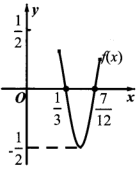 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
17.已知函数f(x)=x3-x+1,则曲线y=f(x)在点(0,1)处的切线与两坐标轴所围成的三角形的面积为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
18.设函数f(x)满足2x2f(x)+x3f'(x)=ex,f(2)=$\frac{e^2}{8}$,则x∈[2,+∞)时,f(x)的最小值为( )
| A. | $\frac{e^2}{2}$ | B. | $\frac{{3{e^2}}}{2}$ | C. | $\frac{e^2}{4}$ | D. | $\frac{e^2}{8}$ |
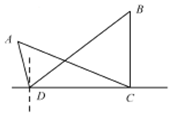 如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.
如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.