题目内容
4.函数$f(x)=\frac{{1+{e^{2x}}}}{{1-{e^{2x}}}}•x$(其中e是自然对数的底数)的大致图象为( )| A. | 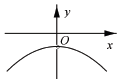 | B. | 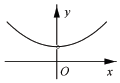 | C. | 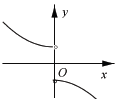 | D. | 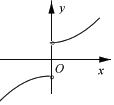 |
分析 根据指数函数的性质判断f(x)的符号,从而得出正确选项.
解答 解:当x<0时,0<e2x<1,∴f(x)<0,
当x>0时,e2x>1,∴f(x)<0,
故选A.
点评 本题考查了函数图象的判断,属于中档题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
14.已知a、b∈R,若3-4i3=$\frac{2-bi}{a+i}$,则a+b等于( )
| A. | -9 | B. | 5 | C. | 13 | D. | 9 |
9.已知复数z满足$z=\frac{1+2i}{{{{(1-i)}^2}}}$,则在复平面内复数$\overline z$对应的点为( )
| A. | $(-1,-\frac{1}{2})$ | B. | $(1,-\frac{1}{2})$ | C. | $(-\frac{1}{2},1)$ | D. | $(-\frac{1}{2},-1)$ |
13.设集合A={x|x>2},B={x|x2-4x<0},则A∩B=( )
| A. | (4,+∞) | B. | (2,4) | C. | (0,4) | D. | (0,2) |
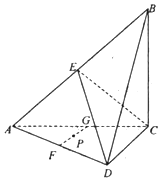 如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.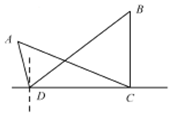 如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.
如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.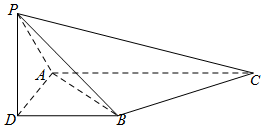 如图,三棱锥P-ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1.
如图,三棱锥P-ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1.