题目内容
9.把3男2女共5名新生分配给甲、乙两个班,每个班分配的新生不少于2名,且甲班至少分配1名女生,则不同的分配方案种数为16.分析 根据题意,用间接法分析:先计算将5人分配到2个班级的情况数目,再分析其中甲班全部为男生的情况数目,用“将5人分配到2个班级”的情况数目减去“甲班没有女生即全部为男生”的情况数目,即可得答案.
解答 解:根据题意,先将5人分配到2个班级,
需要先把5人分成两组,有C52=10种分组方法,再把分好的2组对应2个班级,有A22=2种情况,
则将5人分配到2个班级,有10×2=20种分配方法;
其中甲班没有女生即全部为男生的情况有2种:
甲班只有3名男生,则有C33=1种情况,
甲班只有2名男生,则有C32=3种情况,
则甲班没有女生的即全部为男生的情况有1+3=4种,
则甲班至少分配1名女生的分配方案有20-4=16种;
故答案为:16.
点评 本题考查排列、组合的实际应用,可以选用间接法,避免分类讨论.

练习册系列答案
相关题目
5.在区域$Ω=\left\{{(x,y)|\left\{\begin{array}{l}x≥0\\ x+y≤1\\ x-y≤1\end{array}\right.}\right\}$中,若满足ax+y>0的区域面积占Ω面积的$\frac{1}{3}$,则实数a的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{2}{3}$ |
14.已知a、b∈R,若3-4i3=$\frac{2-bi}{a+i}$,则a+b等于( )
| A. | -9 | B. | 5 | C. | 13 | D. | 9 |
1.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=3,且$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为$\frac{π}{4}$,则|$\overrightarrow{b}$|=( )
| A. | 6 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
| A. | $\frac{2}{3}$钱 | B. | $\frac{5}{6}$钱 | C. | 1钱 | D. | $\frac{7}{6}$钱 |
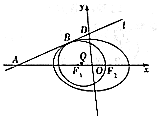 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.