题目内容
给出命题：若cosα=
，则α=
．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）
| 1 |
| 2 |
| π |
| 3 |
| A、3 | B、2 | C、1 | D、0 |
考点：四种命题
专题：简易逻辑
分析：先明确写出原命题的逆命题、否命题、逆否命题，对其三种命题的真假做出判断即可得出答案．
解答：
解：命题：若cosα=
，则α=
．逆命题为：若α=
，则cosα=
为真命题；
否命题为：若cosα≠
，则α≠
为真命题，
逆否命题为：若α≠
，则cosα≠
为假命题，
故真命题有两个，
故选：B．
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
否命题为：若cosα≠
| 1 |
| 2 |
| π |
| 3 |
逆否命题为：若α≠
| π |
| 3 |
| 1 |
| 2 |
故真命题有两个，
故选：B．
点评：本题考查了命题的真假关系，属于基础题，关键是根据原命题能写出它的逆命题、否命题、逆否命题．
练习册系列答案
阅读快车系列答案
相关题目
已知tanα=-
，且α是第二象限角，那么sin（π+α）的值是（ ）
| 4 |
| 3 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
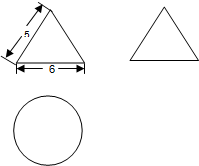一个几何体的三视图及其尺寸如下（单位cm），则该几何体的表面积及体积为（cm2\cm3）（ ）| A、24π，12π |
| B、15π，12π |
| C、24π，36π |
| D、以上都不正确 |
若sin
=
+
（θ∈[0，π]，则tanθ=（ ）
| θ |
| 2 |
| 1+sinθ |
| 1-sinθ |
A、-
| ||
B、
| ||
| C、0 | ||
D、0或-
|
在小于100的自然数中，所有被7除余2的数之和为（ ）
| A、765 | B、665 |
| C、763 | D、663 |
若函数f（x）=
的定义域是（ ）
| (x+1)0 | ||
|
| A、（-∞，-1） |
| B、（-1，0） |
| C、（-1，1） |
| D、（-∞，-1）∪（-1，0） |
函数y=
的定义域为（ ）
| sinx |
| A、[0，π] |
| B、x为第Ⅰ、Ⅱ象限的角 |
| C、{x|2kπ≤x≤（2k+1）π，k∈z} |
| D、（0，π） |