题目内容
在△ABC中,已知a=2
,A=30°,B=45°,解三角形.
| 2 |
考点:正弦定理
专题:解三角形
分析:由三角形的内角和定理求得C,然后直接利用正弦定理得答案.
解答:
解:∵A=30°,B=45°,
∴C=180°-30°-45°=105°,
由
=
,
=
,得
b=
•a=
×2
=
×2
=4,
c=
•a=
×2
=
×2
=2(
+1).
∴C=180°-30°-45°=105°,
由
| a |
| sinA |
| b |
| sinB |
| a |
| sinA |
| c |
| sinC |
b=
| sinB |
| sinA |
| sin45° |
| sin30° |
| 2 |
| ||||
|
| 2 |
c=
| sinC |
| sinA |
| sin105° |
| sin30° |
| 2 |
| ||||||
|
| 2 |
| 3 |
点评:本题考查了解三角形,考查了正弦定理的应用,是基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
给定函数①y=x,②y=log
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
| 1 |
| 2 |
| A、①② | B、②③ | C、③④ | D、①④ |
已知P为椭圆
+
=1(a>b>0)上的任意一点,F1,F2为其焦点,则以PF1为直径的圆与圆x2+y2=a2的位置关系为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、相交 | B、内切 | C、内含 | D、不确定 |
若直线x+y+a=0过圆x2+y2-2x+4y=0的圆心,则a的值为( )
| A、0 | B、-1 | C、2 | D、1 |
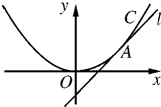 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.