题目内容
已知函数f(x)=
(a、b为常数)
(1)若b=1,解不等式f(x-1)<0;
(2)若a=1,当x∈[-1,2]时,f(x)>
恒成立,求b的取值范围.
| x+a |
| x+b |
(1)若b=1,解不等式f(x-1)<0;
(2)若a=1,当x∈[-1,2]时,f(x)>
| -1 |
| (x+b)2 |
考点:函数恒成立问题,其他不等式的解法
专题:不等式的解法及应用
分析:(1)把b=1代入函数解析式,求出f(x-1),分a<1、a=1、a>1直接求解不等式f(x-1)<0得答案;
(2)把a=1代入f(x)的解析式,把不等式f(x)>
恒成立转化为不等式(x+b)(x+1)>-1成立,分离参数b后利用基本不等式求最值,则b的取值范围可求.
(2)把a=1代入f(x)的解析式,把不等式f(x)>
| -1 |
| (x+b)2 |
解答:
解析:(1)∵f(x)=
,b=1,
∴f(x)=
,
∴f(x-1)=
=
,
∵f(x-1)<0,
∴
<0,等价于x[x-(1-a)]<0,
①当1-a>0,即a<1时,不等式的解集为:(0,1-a),
②当1-a=0,即a=1时,不等式的解集为:x∈∅,
③当1-a<0,即a>1时,不等式的解集为:(1-a,0),
(2)∵a=1,f(x)>
,
∴
>
等价于(x+b)(x+1)>-1.
显然x≠-b,且当x=-1时不等式(x+b)(x+1)>-1成立.
由x∈[-1,2]时不等式恒成立,得
b>-
-x=1-(
+x+1),
∵x+1>0,
∴
+(x+1)≥2
=2.
故b>-1.
| x+a |
| x+b |
∴f(x)=
| x+a |
| x+1 |
∴f(x-1)=
| (x-1)+a |
| (x-1)+1 |
| x-1+a |
| x |
∵f(x-1)<0,
∴
| x-1+a |
| x |
①当1-a>0,即a<1时,不等式的解集为:(0,1-a),
②当1-a=0,即a=1时,不等式的解集为:x∈∅,
③当1-a<0,即a>1时,不等式的解集为:(1-a,0),
(2)∵a=1,f(x)>
| -1 |
| (x+b)2 |
∴
| x+1 |
| x+b |
| -1 |
| (x+b)2 |
显然x≠-b,且当x=-1时不等式(x+b)(x+1)>-1成立.
由x∈[-1,2]时不等式恒成立,得
b>-
| 1 |
| x+1 |
| 1 |
| x+1 |
∵x+1>0,
∴
| 1 |
| x+1 |
|
故b>-1.
点评:本题考查了函数恒成立问题,考查了分类讨论的数学思想方法,考查了分离参数法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列选项中,可作为函数y=f(x)的图象的是( )
A、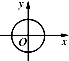 |
B、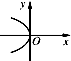 |
C、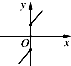 |
D、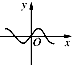 |
设集合M={x|x2+2x-a=0},若M非空,则实数a的取值范围是( )
| A、a≤-1 | B、a≥-1 |
| C、a≤1 | D、a≥1 |