题目内容
已知函数f(2x-1)=4x2,则f(2)= .
考点:函数的值
专题:计算题,函数的性质及应用
分析:令2x-1=2,解得x的值,再把解析式中的x换成此值求得f(2).
解答:
解:由题意得,f(2x-1)=4x2,
令2x-1=2,解得x=
,则f(2)=4×(
)2=9,
故答案为:9.
令2x-1=2,解得x=
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:9.
点评:本题考查求函数的值,以及整体思想,属于基础题.

练习册系列答案
相关题目
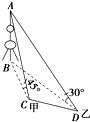 要测量底部不能到达的东方明珠电视塔的高度,在黄浦江西岸选择甲、乙两观测点,在甲、乙两点测得塔顶的仰角分别为45°、30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是( )
要测量底部不能到达的东方明珠电视塔的高度,在黄浦江西岸选择甲、乙两观测点,在甲、乙两点测得塔顶的仰角分别为45°、30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是( )A、100
| ||
| B、400米 | ||
C、200
| ||
| D、500米 |
设a>b,则下列不等式成立的是( )
A、
| ||||
| B、log2a>log2b | ||||
C、
| ||||
| D、2a>2b |
已知集合M={x|sinx>cosx,0<x<π}和N={x|sin2x>cos2x,0<x<π},则M与N的交集为( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|

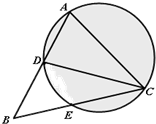 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.