题目内容
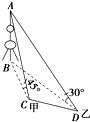要测量底部不能到达的东方明珠电视塔的高度，在黄浦江西岸选择甲、乙两观测点，在甲、乙两点测得塔顶的仰角分别为45°、30°，在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°，甲、乙两地相距500米，则电视塔在这次测量中的高度是（ ）A、100
| ||
| B、400米 | ||
C、200
| ||
| D、500米 |
考点：解三角形的实际应用
专题：应用题,解三角形
分析：先求出BC，BD，再在△BCD中，由余弦定理可得结论．
解答：
解：设塔高AB=hm，在Rt△ABC中，
由已知BC=hm，在Rt△ABD中，由已知BD=
hm，
在△BCD中，
由余弦定理可得3h2=h2+5002-2h•500•cos120°，
即h2-250h-125000=0，
解得h=500（m）（负值舍去）．
故选D．
由已知BC=hm，在Rt△ABD中，由已知BD=
| 3 |
在△BCD中，
由余弦定理可得3h2=h2+5002-2h•500•cos120°，
即h2-250h-125000=0，
解得h=500（m）（负值舍去）．
故选D．
点评：本题考查余弦定理的运用，考查学生的计算能力，正确运用余弦定理是关键．
练习册系列答案
相关题目
已知a为正整数，且关于x的方程lg（4-2x2）=lg（a-x）+1有实根，则a等于（ ）
| A、1 | B、1或2 | C、2 | D、2或3 |
用一个平面去截正方体，则截面不可能是（ ）
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |
已知函数f（x）=ln（1+x）-
，若x≥0时，f（x）≤0，则λ的最小值为（ ）
| x(1+λx) |
| 1+x |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
已知全集M={x||2x-1|≤1，x∈Z}，集合N={3，a}，若M∩N≠∅，则a等于（ ）
| A、1 | B、2 | C、1或2 | D、0或1 |
设F1，F2是双曲线
-
=1的焦点，P是双曲线上一点．若P到F1的距离为9，则P到F2的距离等于（ ）
| x2 |
| 16 |
| y2 |
| 20 |
| A、0 | ||
| B、17 | ||
C、
| ||
| D、2 |
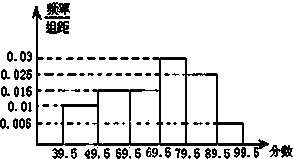如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：