题目内容
设函数f(x)的图象与直线x=a,x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,
]上的面积为
(n∈N*).则
(i)y=sin2x在[0,π]上的面积为 ;
(ii)y=sin(3x-π)+2在[
,
]上的面积为 .
| π |
| n |
| 2 |
| n |
(i)y=sin2x在[0,π]上的面积为
(ii)y=sin(3x-π)+2在[
| π |
| 3 |
| 4π |
| 3 |
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:(i)函数y=sinnx与函数y=sin2x类比,可以得出y=sin2x在[0,π]上的面积.
(ii)设t=x-
,t∈[0,π],则y=sin3t+2,同理可求.
(ii)设t=x-
| π |
| 3 |
解答:
解:(i)∵函数y=sinnx在[0,
]上的面积为
(n∈N*),∴对于函数y=sin2x而言,n=2,
∴y=sin2x在[0,π]上的面积为1;
(ii)设t=x-
,t∈[0,π],则y=sin3t+2,∴y=sin(3x-π)+2在[
,
]的面积为2π+
故答案为:1;2π+
.
| π |
| n |
| 2 |
| n |
∴y=sin2x在[0,π]上的面积为1;
(ii)设t=x-
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| 2 |
| 3 |
故答案为:1;2π+
| 2 |
| 3 |
点评:在解题过程中,寻找解题的突破口,往往离不开类比联想,我们在解题中,要进一步通过概念类比、性质类比、结构类比以及方法类比等思维训练途径,来提高类比推理的能力,培养探究创新精神.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为( )A、6
| ||
B、4
| ||
| C、6 | ||
| D、4 |

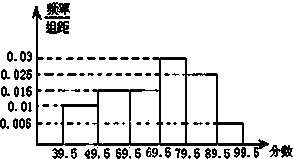 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: