题目内容
小白被“老大”找到了!小伙伴们喜大普奔啊有木有!为了答谢“老大”,小新他们决定帮助“老大”做一件事,就是调查双叶幼稚园小朋友在20:00~21:00时间段在做什么?最后小新等做成了下面的数据表:
(1)将此样本的频率作为总体的概率估计,随机调查3名男性小朋友,设调查的3名男性小朋友在这一时间段以看电视的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,吉永老师能否有99%的把握认为“在20:00~21:00时间段的休闲方式与性别有关系”?
参考公式:K=
,其中n=a+b+c+d.
参考数据:
 | 看电视 | 看书 | 合计 |
| 男 | 25 | 5 | 30 |
| 女 | 10 | 10 | 20 |
| 合计 | 35 | 15 | 50 |
(2)根据以上数据,吉永老师能否有99%的把握认为“在20:00~21:00时间段的休闲方式与性别有关系”?
参考公式:K=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
考点:独立性检验的应用
专题:综合题,概率与统计
分析:(1)由表中看出随机变量X服从二项分布,运用独立重复试验公式求出概率后列出分布列,运用二项分布公式求X的期望;
(2)根据计算出的临界值,同临界值表进行比较,得到假设不合理的程度约为99%.
(2)根据计算出的临界值,同临界值表进行比较,得到假设不合理的程度约为99%.
解答:
解:根据题意可得X~B(3,
),∴P(X=k)=
(
)3-k(
)k,k=0,1,2,3.
∴E(X)=np=3×
=
.
(2)提出假设H0:休闲方式与性别无关系,
根据样本提供的2×2列联表得k=
≈6.34<6.635,
故没有99%的把握认为“在20:00~22:00时间段的休闲方式与性别有关系”.
| 5 |
| 6 |
| C | k 3 |
| 1 |
| 6 |
| 5 |
| 6 |
∴E(X)=np=3×
| 5 |
| 6 |
| 5 |
| 2 |
(2)提出假设H0:休闲方式与性别无关系,
根据样本提供的2×2列联表得k=
| 50×(25×10-10×5)2 |
| 35×15×30×20 |
故没有99%的把握认为“在20:00~22:00时间段的休闲方式与性别有关系”.
点评:本题是一个独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.

练习册系列答案
相关题目
用一个平面去截正方体,则截面不可能是( )
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |
设F1,F2是双曲线
-
=1的焦点,P是双曲线上一点.若P到F1的距离为9,则P到F2的距离等于( )
| x2 |
| 16 |
| y2 |
| 20 |
| A、0 | ||
| B、17 | ||
C、
| ||
| D、2 |
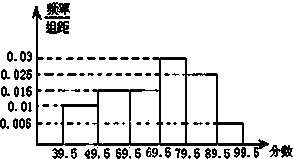 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: