题目内容
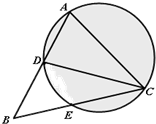 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于E,AB=2BE.(Ⅰ)求证:BC=2BD;
(Ⅱ)若CD平分∠ACB,且AC=2,EC=1,求BD的长.
考点:与圆有关的比例线段
专题:综合题,立体几何
分析:(Ⅰ)连接DE,证明△DBE∽△CBA,即可证明BC=2BD;
(Ⅱ)先求DE,利用CD是∠ACB的平分线,可得DA=1,根据割线定理求出BD.
(Ⅱ)先求DE,利用CD是∠ACB的平分线,可得DA=1,根据割线定理求出BD.
解答:
(Ⅰ)证明:连接DE,∵四边形ABCD 是圆的内接四边形,
∴∠BDE=∠BCA,又∠DBE=∠CBA,∴△DBE∽△CBA,
∴
=
,
又AB=2BE,∴BC=2BD …(5分)
(Ⅱ)由(Ⅰ)△DBE∽△CBA,知
=
,
又AB=2BE,∴AC=2DE,
∵AC=2,∴DE=1,而CD 是∠ACB 的平分线,∴DA=1,
设BD=x,根据割线定理得BD•BA=BE•BC
即x(x+1)=
(x+1)[
(x+1)+1],
解得x=1,即BD=1 …(10分)
∴∠BDE=∠BCA,又∠DBE=∠CBA,∴△DBE∽△CBA,
∴
| BE |
| AB |
| BD |
| BC |
又AB=2BE,∴BC=2BD …(5分)
(Ⅱ)由(Ⅰ)△DBE∽△CBA,知
| BE |
| AB |
| ED |
| AC |
又AB=2BE,∴AC=2DE,
∵AC=2,∴DE=1,而CD 是∠ACB 的平分线,∴DA=1,
设BD=x,根据割线定理得BD•BA=BE•BC
即x(x+1)=
| 1 |
| 2 |
| 1 |
| 2 |
解得x=1,即BD=1 …(10分)
点评:本题考查与圆有关的比例线段,考查割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=ln(1+x)-
,若x≥0时,f(x)≤0,则λ的最小值为( )
| x(1+λx) |
| 1+x |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
已知幂函数y=f(x)的图象经过点(8,
),则f(
)的值为( )
| 1 |
| 2 |
| 1 |
| 64 |
| A、3 | ||
B、
| ||
| C、4 | ||
D、
|
f(x)是偶函数,定义域是(-∞,+∞),在[0,+∞)上f(x)是减函数,那么f(-
)与f(a2-a+1)(a∈R)的大小关系是( )
| 3 |
| 4 |
A、f(-
| ||
B、f(-
| ||
C、f(-
| ||
D、f(-
|
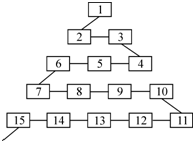 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则