题目内容
对任意实数x，不等式|x-1|-|x-2|＞a恒成立，则a的取值范围是 ．
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：要使不等式|x-1|-|x-2|＞a成立，需f（x）=|x-1|-|x-2|的最小值大于a，问题转化为求f（x）的最小值．
解答：
解：对任意实数x，不等式|x-1|-|x-2|＞a恒成立，而|x-1|-|x-2|表示数轴上的x对应点到1对应点的距离减去它到2对应点的距离，
其最小值为-1，故有a＜-1，
故答案为：{a|a＜-1}．
其最小值为-1，故有a＜-1，
故答案为：{a|a＜-1}．
点评：本题主要考查绝对值的意义，绝对值不等式的解法，属于中档题．
练习册系列答案
相关题目
已知全集M={x||2x-1|≤1，x∈Z}，集合N={3，a}，若M∩N≠∅，则a等于（ ）
| A、1 | B、2 | C、1或2 | D、0或1 |
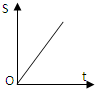
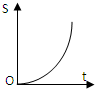
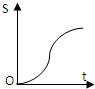
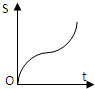
如图，正方形街道OABC，已知小白从A出发，沿着正方形边缘A-B-C匀速走动，小白与O连线扫过的正方形内阴影部分面积S是时间t的函数，这个函数的大致图象是（ ）
