题目内容
已知x＞0，则函数y=
的最大值为 ．
| 4x |
| x2+1 |
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：y=
=
，利用基本不等式，即可得出结论．
| 4x |
| x2+1 |
| 4 | ||
x+
|
解答：
解：y=
=
，
∵x＞0，
∴x+
≥2，
∴0＜
≤2，
∴函数y=
的最大值为2．
故答案为：2．
| 4x |
| x2+1 |
| 4 | ||
x+
|
∵x＞0，
∴x+
| 1 |
| x |
∴0＜
| 4 | ||
x+
|
∴函数y=
| 4x |
| x2+1 |
故答案为：2．
点评：本题考查基本不等式在最值问题中的应用，比较基础．
练习册系列答案
相关题目
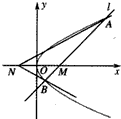已知过点M（a，0）（a＞0）的动直线l交抛物线y2=4x于A、B两点，点N与点M关于y轴对称，