题目内容
下面几种推理中是演绎推理的序号为（ ）
| A、半径为r圆的面积S=πr2，则单位圆的面积S=π |
| B、由金、银、铜、铁可导电，猜想：金属都可导电 |
| C、由平面三角形的性质，推测空间四面体性质 |
| D、由平面直角坐标系中圆的方程为（x-a）2+（y-b）2=r2，推测空间直角坐标系中球的方程为（x-a）2+（y-b）2+（z-c）2 |
考点：演绎推理的基本方法
专题：推理和证明
分析：根据演绎推理，归纳推理和类比推理的概念，判定每一个选项是否符合条件即可．
解答：
解：对于A，根据演绎推理的三段论知，大前提是半径为r圆的面积S=πr2，小前提是单位圆是半径为1的圆，结论是单位圆的面积S=π，∴A是演绎推理；
对于B，是由特殊到一般，是归纳推理；
对于C，是由一类事物的特征，得出另一类事物的特征，是类比推理；
对于D，是由一类事物的特征，得出另一类事物的特征，是类比推理．
故选：A．
对于B，是由特殊到一般，是归纳推理；
对于C，是由一类事物的特征，得出另一类事物的特征，是类比推理；
对于D，是由一类事物的特征，得出另一类事物的特征，是类比推理．
故选：A．
点评：本题考查了演绎推理，归纳推理和类比推理的应用问题，解题时应根据演绎推理，归纳推理和类比推理的概念，对每一个选项逐一判定即可，是基础题．
练习册系列答案
相关题目
函数y=3sinx+2cosx的最小值是（ ）
| A、0 | ||
| B、-3 | ||
| C、-5 | ||
D、-
|
设M是椭圆
+
=1上的一点，F1、F2为焦点，∠F1MF2=
，则S△ MF1F2为（ ）
| x2 |
| 25 |
| y2 |
| 16 |
| π |
| 3 |
A、
| ||||
B、16
| ||||
C、
| ||||
D、25
|
已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
在Rt△ABC中，A=90°，AB=1，则
•
的值是（ ）
| AB |
| BC |
| A、1 |
| B、-1 |
| C、1或-1 |
| D、不确定，与B的大小，BC的长度有关 |
将函数y=sin（3x+
）的图象向左平移
个单位，再将所得图象上所有点的横坐标缩短到原来的
倍（纵坐标不变），则所得图象的函数解析式为（ ）
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
A、y=sin（
| ||||
B、y=sin（6x+
| ||||
| C、y=sin6x | ||||
D、y=sin（6x+
|
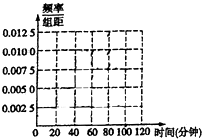某中学为研究学生的身体素质与课外体育锻炼时间的关系，对400名高一学生的一周课外体育锻炼时间进行调查，结果如下表所示：