题目内容
在Rt△ABC中，A=90°，AB=1，则
•
的值是（ ）
| AB |
| BC |
| A、1 |
| B、-1 |
| C、1或-1 |
| D、不确定，与B的大小，BC的长度有关 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：直接利用向量的数量积求解即可．
解答：
解：在Rt△ABC中，A=90°，AB=1，则
•
=|
|•|
|cos（π-B）=-AB2=-1．
故选：B．
| AB |
| BC |
| AB |
| BC |
故选：B．
点评：本题考查平面向量的数量积的运算，基本知识的考查．
练习册系列答案
相关题目
运行程序框图所对应的程序，输出结果s的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知直线l的方程为3x-y+3=0，则l在y轴上的截距为（ ）
| A、-3 | B、3 | C、-5 | D、5 |
下面几种推理中是演绎推理的序号为（ ）
| A、半径为r圆的面积S=πr2，则单位圆的面积S=π |
| B、由金、银、铜、铁可导电，猜想：金属都可导电 |
| C、由平面三角形的性质，推测空间四面体性质 |
| D、由平面直角坐标系中圆的方程为（x-a）2+（y-b）2=r2，推测空间直角坐标系中球的方程为（x-a）2+（y-b）2+（z-c）2 |
sin
的值为（ ）
| 37π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若椭圆经过原点，且焦点分别为F1（0，1），F2（0，3）则该椭圆的短轴长为（ ）
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
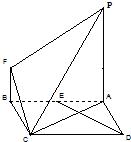如图，正方形ABCD边长为2，PA⊥平面ABCD，BF∥PA，BF=