题目内容
给出下列函数（1）y=x2+|x|+2，x≤0（2）y=t2-t+2，t≤0（3）y=x2-|x|+2，x≥0（4）y=（
）4+
+2，其中与函数y=x2-x+2，x≤0相等的有（ ）
| x |
| x2 |
| A、（1） |
| B、（1）（2） |
| C、（1）（2）（4） |
| D、（1）（3）（4） |
考点：二次函数的性质
专题：函数的性质及应用
分析：分别判断四个函数的定义域和对应法则是否相同即可．
解答：
解：（1）y=x2+|x|+2=x2-x+2，x≤0，定义域和对应法则，与函数y=x2-x+2，x≤0一致，故为同一函数；
（2）y=t2-t+2，t≤0，定义域和对应法则，与函数y=x2-x+2，x≤0一致，故为同一函数；
（3）y=x2-|x|+2=x2+x+2，x≥0，定义域与函数y=x2-x+2，x≤0不一致，故不为同一函数；
（4）y=（
）4+
+2=x2+x+2，x≥0，定义域与函数y=x2-x+2，x≤0不一致，故不为同一函数；
故与函数y=x2-x+2，x≤0相等的有（1）（2），
故选：B
（2）y=t2-t+2，t≤0，定义域和对应法则，与函数y=x2-x+2，x≤0一致，故为同一函数；
（3）y=x2-|x|+2=x2+x+2，x≥0，定义域与函数y=x2-x+2，x≤0不一致，故不为同一函数；
（4）y=（
| x |
| x2 |
故与函数y=x2-x+2，x≤0相等的有（1）（2），
故选：B
点评：本题主要考查判断两个函数是否是相同函数，判断的标准是判断函数的定义域和对应法则是否一致．
练习册系列答案
相关题目
已知函数f（x）=（1+cos2x）sin2x，x∈R，则f（x）是（ ）
| A、最小正周期为π的奇函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的偶函数 | ||
D、最小正周期为
|
点P在直线x+y-4=0上，O为原点，则|OP|的最小值是（ ）
| A、2 | ||
B、
| ||
C、2
| ||
D、
|
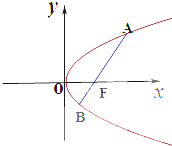如图，给定抛物线C：y2=4x，F是C的焦点，过点F的直线l与C相交于A、B两点，O为坐标原点