题目内容
点P在直线x+y-4=0上,O为原点,则|OP|的最小值是( )
| A、2 | ||
B、
| ||
C、2
| ||
D、
|
考点:点到直线的距离公式
专题:直线与圆
分析:直接由点到直线的距离公式求|OP|的最小值.
解答:
解:由点到直线的距离公式得:|OP|的最小值=
=2
.
故选:C.
| |-4| | ||
|
| 2 |
故选:C.
点评:本题考查了得到直线的距离公式,体现了数学转化思想方法,是基础的计算题.

练习册系列答案
相关题目
给出下列函数(1)y=x2+|x|+2,x≤0(2)y=t2-t+2,t≤0(3)y=x2-|x|+2,x≥0(4)y=(
)4+
+2,其中与函数y=x2-x+2,x≤0相等的有( )
| x |
| x2 |
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(4) |
| D、(1)(3)(4) |
已知x4=81,那么x等于( )
| A、3 | B、-3 |
| C、-3或3 | D、不存在 |
已知定义在R上的奇函数f(x),且为减函数,又知f(1-a)+f(1-a2)<0,则a的取值范围为( )
| A、(-2,1) |
| B、(-∞,-2)∪(1,+∞) |
| C、(0,1) |
| D、(0,2) |
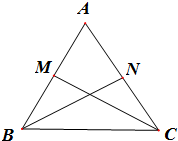 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.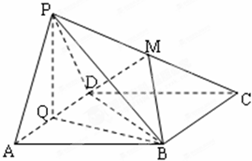 如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.