题目内容
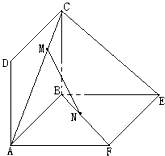
如图,正方形ABCD、ABEF的边长都是1,且∠CBE=90°,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
)
(1)能否说明对任意a∈(0,
),恒有MN∥平面CBE?
(2)当a为何值时,MN的长最短?
| 2 |

(1)能否说明对任意a∈(0,
| 2 |
(2)当a为何值时,MN的长最短?
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连接PQ,证明MNQP是平行四边形.然后证明MN∥平面CBE且与a的大小关系无关.
(2)由(1)MN=PQ,CM=BN=a,脱光光
=
,
=
,求出MN的表达式,然后求解最小值.
(2)由(1)MN=PQ,CM=BN=a,脱光光
| CP |
| 1 |
| a | ||
|
| BQ |
| 1 |
| a | ||
|
解答:
解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连接PQ,
依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形.
PQ?平面CBE,MN?平面CBE,MN∥平面CBE且与a的大小关系无关.
(2)由(1)MN=PQ,CM=BN=a,AC=BF=
,
=
,
=
,CP=BQ=
a
MN=PQ=
=
=
,(0<a<
)
∴当a=
,即当M、N分别为AC、BF的中点时,MN的长最小,最小值为
.
依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形.
PQ?平面CBE,MN?平面CBE,MN∥平面CBE且与a的大小关系无关.
(2)由(1)MN=PQ,CM=BN=a,AC=BF=
| 2 |
| CP |
| 1 |
| a | ||
|
| BQ |
| 1 |
| a | ||
|
| ||
| 2 |
MN=PQ=
| (1-CP)2+BQ2) |
(a-
|
1-
|
| 2 |
∴当a=
| ||
| 2 |
| ||
| 2 |
点评:本题考查直线与平面平行的判定定理的应用,空间两点间距离公式求解最值问题,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
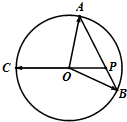 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
给出下列函数(1)y=x2+|x|+2,x≤0(2)y=t2-t+2,t≤0(3)y=x2-|x|+2,x≥0(4)y=(
)4+
+2,其中与函数y=x2-x+2,x≤0相等的有( )
| x |
| x2 |
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(4) |
| D、(1)(3)(4) |
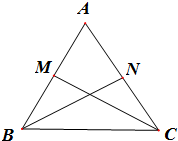 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.