题目内容
已知函数f(x)=
x2-alnx,若函数y=f(x)的图象在点P(2,f(2))处的切线方程为l:y=x+b.
(1)求出实数a,b的值;
(2)当x∈[
, e]时,不等式f(x)<k恒成立,求实数k的取值范围.
| 1 |
| 2 |
(1)求出实数a,b的值;
(2)当x∈[
| 1 |
| e |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求出原函数的导函数,由f′(2)=1求得a的值,求出f(2),再由点P在直线上解得b的值;
(2)利用导数求出函数f(x)在[
,e]上的最值,则实数k的取值范围可求.
(2)利用导数求出函数f(x)在[
| 1 |
| e |
解答:
解:(1)∵f(x)=
x2-alnx,
∴f'(x)=x-
,
∴f'(2)=2-
=1⇒a=2.
∴f(x)=
x2-2lnx.
∵点P坐标满足f(x)=
x2-2lnx,
∴f(2)=2-2ln2,
∵点P在直线l上,∴b=-2ln2,
∴a=2,b=-2ln2;
(2)由(1)知f(x)=
x2-2lnx.
∴f′(x)=x-
=
,
由f'(x)=0⇒x=
(x=-
舍去).
∴当x∈[
,
]时,f(x)为减函数,当x∈[
,e]时,f(x)为增函数.
又f(
)=2+
, f(e)=
e2-2⇒f(
)>f(e),
故当x∈[
,e]时,函数y=f(x)的最大值为2+
,
∴k>2+
.
| 1 |
| 2 |
∴f'(x)=x-
| a |
| x |
∴f'(2)=2-
| a |
| 2 |
∴f(x)=
| 1 |
| 2 |
∵点P坐标满足f(x)=
| 1 |
| 2 |
∴f(2)=2-2ln2,
∵点P在直线l上,∴b=-2ln2,
∴a=2,b=-2ln2;
(2)由(1)知f(x)=
| 1 |
| 2 |
∴f′(x)=x-
| 2 |
| x |
(x-
| ||||
| x |
由f'(x)=0⇒x=
| 2 |
| 2 |
∴当x∈[
| 1 |
| e |
| 2 |
| 2 |
又f(
| 1 |
| e |
| 1 |
| 2e2 |
| 1 |
| 2 |
| 1 |
| e |
故当x∈[
| 1 |
| e |
| 1 |
| 2e2 |
∴k>2+
| 1 |
| 2e2 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,是中档题.

练习册系列答案
相关题目
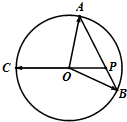 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
不等式组
的解集记为D,由下面四个命题:
P1:?(x,y)∈D,则2x-y≥-1;
P2:?(x,y)∈D,则2x-y<-2;
P3:?(x,y)∈D,则2x-y>7;
P4:?(x,y)∈D,则2x-y≤5.
其中正确命题是( )
|
P1:?(x,y)∈D,则2x-y≥-1;
P2:?(x,y)∈D,则2x-y<-2;
P3:?(x,y)∈D,则2x-y>7;
P4:?(x,y)∈D,则2x-y≤5.
其中正确命题是( )
| A、P2,P3 |
| B、P1,P2 |
| C、P1,P3 |
| D、P1,P4 |
给出下列函数(1)y=x2+|x|+2,x≤0(2)y=t2-t+2,t≤0(3)y=x2-|x|+2,x≥0(4)y=(
)4+
+2,其中与函数y=x2-x+2,x≤0相等的有( )
| x |
| x2 |
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(4) |
| D、(1)(3)(4) |
已知x4=81,那么x等于( )
| A、3 | B、-3 |
| C、-3或3 | D、不存在 |
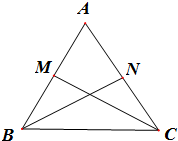 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.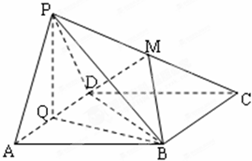 如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.