题目内容
当x>-1时,不等式 x+
+1≥a恒成立,则实数a的最大值是 .
| 1 |
| x+1 |
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:根据基本不等式的性质求出x+
+1的最小值为2,再根据当x>-1时,不等式x+
+1≥a恒成立,求出a的范围,继而问题得以解决.
| 1 |
| x+1 |
| 1 |
| x+1 |
解答:
解:∵x>-1,
∴x+1>0,
∴x+
+1=x+1+
≥2
=2,当且仅当x=0时取等号,
∴x+
+1的最小值为2,
∵不等式x+
+1≥a恒成立,
∴a≤2,
∴实数a的最大值是2.
故答案为:2.
∴x+1>0,
∴x+
| 1 |
| x+1 |
| 1 |
| x+1 |
(x+1)•
|
∴x+
| 1 |
| x+1 |
∵不等式x+
| 1 |
| x+1 |
∴a≤2,
∴实数a的最大值是2.
故答案为:2.
点评:本题考查函数恒成立问题,关键是利用基本不等式,注意等号成立的条件,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
在△ABC中,若c=2acosB,则△ABC的形状为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |
给出下列函数(1)y=x2+|x|+2,x≤0(2)y=t2-t+2,t≤0(3)y=x2-|x|+2,x≥0(4)y=(
)4+
+2,其中与函数y=x2-x+2,x≤0相等的有( )
| x |
| x2 |
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(4) |
| D、(1)(3)(4) |
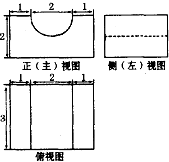
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
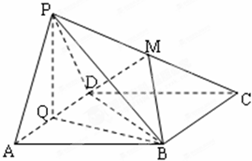 如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.