题目内容
若不等式
≥
(x∈R)对任意实数x都成立,则正实数m取值范围为 .
| x2+1+m | ||
|
| 1+m | ||
|
考点:函数恒成立问题
专题:计算题,综合题,不等式的解法及应用
分析:
≥
即
+
≥
,令t=
,t≥
,则不等式可化为t+
≥
,从而不等式等价于(t+
)min≥
,利用导数可求得(t+
)min,注意讨论m的范围.
| x2+1+m | ||
|
| 1+m | ||
|
| x2+m |
| 1 | ||
|
| 1+m | ||
|
| x2+m |
| m |
| 1 |
| t |
| 1+m | ||
|
| 1 |
| t |
| 1+m | ||
|
| 1 |
| t |
解答:
解:
≥
即
+
≥
,
令t=
,t≥
,则不等式可化为t+
≥
,
令y=t+
,则y′=1-
=
,
①当0<m<1时,若
≤t<1,y′<0,若t>1,y′>0,
∴t=1时,ymin=2,
∴2≥
,(
-1)2≤0,无解;
②当m≥1时,y′=
≥0,
y=t+
在[
,+∞]上为增函数,
∴ymin=
+
≥
,该不等式恒成立,
∴m≥1,
综上,m≥1.
故答案为:m≥1.
| x2+1+m | ||
|
| 1+m | ||
|
| x2+m |
| 1 | ||
|
| 1+m | ||
|
令t=
| x2+m |
| m |
| 1 |
| t |
| 1+m | ||
|
令y=t+
| 1 |
| t |
| 1 |
| t2 |
| (t+1)(t-1) |
| t2 |
①当0<m<1时,若
| m |
∴t=1时,ymin=2,
∴2≥
| 1+m | ||
|
| m |
②当m≥1时,y′=
| (t+1)(t-1) |
| t2 |
y=t+
| 1 |
| t |
| m |
∴ymin=
| 1 | ||
|
| m |
| 1+m | ||
|
∴m≥1,
综上,m≥1.
故答案为:m≥1.
点评:本题考查函数恒成立问题、利用导数求函数的最值,考查转化思想、分类讨论思想,转化为函数最值是解决恒成立问题的常用方法,注意体会.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
下列命题为真命题的是( )
| A、椭圆的离心率大于1 | ||||
B、双曲线
| ||||
C、?a,b∈R,
| ||||
D、?x∈R,sinx+cosx=
|
已知集合A={x|x2-5x-6<0},B={x||x|<2},则A∩(∁RB)=( )
| A、(-1,2) |
| B、[-1,2) |
| C、(2,6) |
| D、[2,6) |
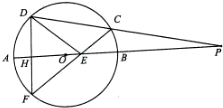 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.