题目内容
设数列{an}的前n项的和Sn与an的关系是Sn=-an+1-
,n∈N*.
(Ⅰ)求a1,a2a3并归纳出数列{an}的通项(不需证明);
(Ⅱ)求数列{Sn}的前n项和Tn.
| 1 |
| 2n |
(Ⅰ)求a1,a2a3并归纳出数列{an}的通项(不需证明);
(Ⅱ)求数列{Sn}的前n项和Tn.
考点:数列的求和,数列的概念及简单表示法
专题:等差数列与等比数列
分析:(Ⅰ)根据已知条件,利用递推思想依次求出a1,a2a3,总结规律能归纳出数列{an}的通项.
(Ⅱ)由an=
,利用错位相减法能求出Sn=1-
,再利用错位相减法能求出数列{Sn}的前n项和Tn.
(Ⅱ)由an=
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
解答:
解:(Ⅰ)∵Sn=-an+1-
,n∈N*,
∴a1=-a1+1-
,解得a1=
=
,
S2=
+a2=-a2+1-
,解得a2=
=
,
S3=
+
+a3=-a3+1-
,解得a3=
,
由此猜想an=
.
用数学归纳法证明:
①当n=1时,a1=
,成立,
②假设n=k时成立,即ak=
,
则当n=k+1时,Sk+1=
+
+…+
+ak+1=-ak+1+1-
,
设S=
+
+…+
,①
则
S=
+
+…+
,②
①-②,得
S=
+
+
+…+
-
=
-
=
-
,
∴S=1-
,
∴2ak+1=1-
-1+
=
,
∴ak+1=
,成立,
∴an=
.
(Ⅱ)∵an=
,
∴Sn=
+
+
+…+
,③
Sn=
+
+
+…+
,④
③-④得:
Sn=
+
+…+
-
=
-
=
-
-
,
∴Sn=1-
,
∴Tn=n-(
+
+…+
),⑤
Tn=
-(
+
+…+
),⑥
⑤-⑥,得
Tn=
-(
+
+
+…+
-
)
=
-[
+
-
]
=
-
-
+
+
=
-1+
+
,
∴Tn=n-2+
.
| 1 |
| 2n |
∴a1=-a1+1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 22 |
S2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 23 |
S3=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 23 |
| 3 |
| 24 |
由此猜想an=
| n |
| 2n+1 |
用数学归纳法证明:
①当n=1时,a1=
| 1 |
| 22 |
②假设n=k时成立,即ak=
| k |
| 2k+1 |
则当n=k+1时,Sk+1=
| 1 |
| 22 |
| 2 |
| 23 |
| k |
| 2k+1 |
| 1 |
| 2k+1 |
设S=
| 1 |
| 22 |
| 2 |
| 23 |
| k |
| 2k+1 |
则
| 1 |
| 2 |
| 1 |
| 23 |
| 2 |
| 24 |
| k |
| 2k+2 |
①-②,得
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2k+1 |
| k |
| 2k+2 |
=
| ||||
1-
|
| k |
| 2k+2 |
=
| 1 |
| 2 |
| 2+k |
| 2k+2 |
∴S=1-
| 2+k |
| 2k+1 |
∴2ak+1=1-
| 1 |
| 2k+1 |
| 2+k |
| 2k+1 |
| k+1 |
| 2k+1 |
∴ak+1=
| k+1 |
| 2k+2 |
∴an=
| n |
| 2n+1 |
(Ⅱ)∵an=
| n |
| 2n+1 |
∴Sn=
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 23 |
| 2 |
| 24 |
| 3 |
| 25 |
| n |
| 2n+2 |
③-④得:
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n+1 |
| n |
| 2n+2 |
=
| ||||
1-
|
| n |
| 2n+2 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+2 |
∴Sn=1-
| n+2 |
| 2n+1 |
∴Tn=n-(
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
| 1 |
| 2 |
| n |
| 2 |
| 3 |
| 23 |
| 4 |
| 24 |
| n+2 |
| 2n+2 |
⑤-⑥,得
| 1 |
| 2 |
| n |
| 2 |
| 3 |
| 4 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
=
| n |
| 2 |
| 3 |
| 4 |
| ||||
1-
|
| n+2 |
| 2n+2 |
=
| n |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
=
| n |
| 2 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+1 |
∴Tn=n-2+
| n+4 |
| 2n+1 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
已知集合A={x|x2-5x-6<0},B={x||x|<2},则A∩(∁RB)=( )
| A、(-1,2) |
| B、[-1,2) |
| C、(2,6) |
| D、[2,6) |
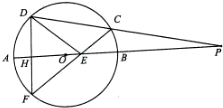 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E. 某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.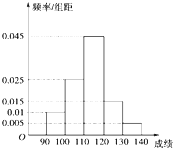 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.