题目内容
曲线y=x2-x+1在点(1,0)处的切线方程为( )
| A、y=x-1 |
| B、y=-x+1 |
| C、y=2x-2 |
| D、y=-2x+2 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,得到函数在x=1处的导数,然后代入直线方程的点斜式得答案.
解答:
解:∵y=x2-x+1,
∴y′=2x-1,
y′|x=1=1,
∴曲线y=x2-x+1在点(1,0)处的切线方程为y-0=1×(x-1),
即y=x-1.
故选:A.
∴y′=2x-1,
y′|x=1=1,
∴曲线y=x2-x+1在点(1,0)处的切线方程为y-0=1×(x-1),
即y=x-1.
故选:A.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
tan1815°+cot
=( )
| 13π |
| 12 |
| A、2 | ||||
| B、2 | ||||
| C、4 | ||||
D、
|
二次不等式ax2+bx+c<0的解集为{x|x≠-
}的条件为( )
| b |
| 2a |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
等比数列{an}中,a1•a5=16,则a3=( )
| A、8 | B、4 | C、-4 | D、±4 |
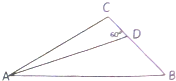 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?