题目内容
将函数y=2sin(
-2x)(x∈[0,π])向左平移
个单位长度,则平移后函数的单调递增区间是( )
| π |
| 3 |
| π |
| 6 |
A、[-
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由题意根据函数y=Asin(ωx+φ)的图象变换规律可得平移后函数的解析式为y=-2sin2x,x∈[-
,
],则平移后函数的单调递增区间是平移后y=sin2x的减区间,从而得出结论.
| π |
| 6 |
| 5π |
| 6 |
解答:
解:将函数y=2sin(
-2x)=-sin(2x-
)(x∈[0,π])向左平移
个单位长度,
则平移后函数的解析式为y=-2sin[2(x+
)-
]=-2sin2x,x∈[-
,
],
则平移后函数的单调递增区间是平移后y=sin2x的减区间,
即[
,
],
故选:C.
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
则平移后函数的解析式为y=-2sin[2(x+
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
则平移后函数的单调递增区间是平移后y=sin2x的减区间,
即[
| π |
| 4 |
| 3π |
| 4 |
故选:C.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的减区间,体现了转化的数学思想,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知数列{an},an=-2n2+λn,若该数列是递减数列,则实数λ的取值范围是( )
| A、(-∞,6) |
| B、(-∞,4] |
| C、(-∞,5) |
| D、(-∞,3] |
设函数f(x)=sin(2x+φ)(0<φ<π),f(x)图象的一条对称轴是x=
,则φ的值为( )
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=3ex-x2ex-a在R上存在三个零点,则实数a的取值范围为( )
| A、[6e-3,2e] |
| B、(0,2e] |
| C、(-6e-3,0) |
| D、(-6e-3,2e) |
若复数
+
(i为虚数单位)的实部与虚部互为相反数,则实数a的值为( )
| a |
| 1-i |
| 1-i |
| 2 |
| A、2 | B、1 | C、-1 | D、0 |
已知函数f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
| A、1007 | B、2014 |
| C、2015 | D、4028 |
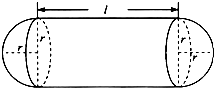 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.