题目内容
已知函数f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
| A、1007 | B、2014 |
| C、2015 | D、4028 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数的奇偶性的性质得到f(x)+f(1-x)=0,从而得到g(x)+g(1-x)=f(x)+f(1-x)+2=2为常数,即可得到结论.
解答:
解:∵函数f(x+
)为奇函数,
∴f(-x+
)=-f(x+
),即函数f(-x+
+
)=-f(x-
+
),
即f(1-x)=-f(x),
则f(x)+f(1-x)=0,
∵g(x)=f(x)+1,
∴g(1-x)=f(1-x)+1,
则g(x)+g(1-x)=f(x)+f(1-x)+2=2,
则g(
)+g(
)+g(
)+g(
)+…+g(
)=1007×2=2014,
故选:B.
| 1 |
| 2 |
∴f(-x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即f(1-x)=-f(x),
则f(x)+f(1-x)=0,
∵g(x)=f(x)+1,
∴g(1-x)=f(1-x)+1,
则g(x)+g(1-x)=f(x)+f(1-x)+2=2,
则g(
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
故选:B.
点评:本题主要考查函数值的计算.利用函数奇偶性的性质得到g(x)+g(1-x)=2为常数是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设z=x+ky,其中x,y满足
,当z的最小值为-
时,k的值为( )
|
| 3 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
将函数y=2sin(
-2x)(x∈[0,π])向左平移
个单位长度,则平移后函数的单调递增区间是( )
| π |
| 3 |
| π |
| 6 |
A、[-
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
若实数x、y满足
,则2x-3y的最值情况是( )
|
| A、最大值为2,最小值为-4 |
| B、最大值为2,无最小值 |
| C、无最大值,最小值为-4 |
| D、既无最大值,又无最小值 |
若复数
-1(a为实数,i为虚数单位)是纯虚数,则a=( )
| a+i |
| 3+4i |
| A、7 | ||
| B、-7 | ||
C、
| ||
D、-
|
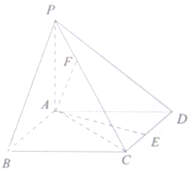 如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.
如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.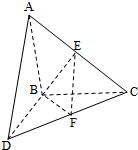 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.