Question

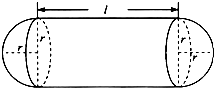某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为

80

3

π立方米，且l≥2r．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为22千元．设该容器的建造费用为y千元．当该容器建造费用最小时，r的值为（　　）

• A、

  1

  2

• B、1
• C、

  3

  2

• D、2

Answer 1

考点：函数最值的应用,根据实际问题选择函数类型

专题：函数的性质及应用,不等式的解法及应用

分析：由圆柱和球的体积的表达式，得到l和r的关系．再由圆柱和球的表面积公式建立关系式，将表达式中的l用r表示，进而求出建造费用y的表达式，利用基本不等式可求出该容器建造费用最小时，r的值．

解答： 解：（1）由体积V=

4

3

πr³+πr²l=

80π

3

，
解得l=

V- 4 3 πr2

πr2

=

4

3

(

20

r2

-r)，
∴建造费用y=2πrl×3+4πr²×22=2πr×

4

3

(

20

r2

-r)×3+4πr²×22，
∴y=80πr²+

160π

r

≥80π（3×

3	r2• 1 r • 1 r

）=240π，
当且仅当，r=1时，取等号，
故该容器建造费用最小时，r的值为1，
故选：B

点评：本题考查的知识点是函数最值的应用，其中根据已知求出建造费用y的表达式，是解答的关键．