题目内容
设函数f（x）=sin（2x+φ）（0＜φ＜π），f（x）图象的一条对称轴是x=
，则φ的值为（ ）
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用正弦函数的对称性可得2×
+φ=kπ+
（k∈Z），又0＜φ＜π，于是可求得答案．
| π |
| 8 |
| π |
| 2 |
解答：
解：∵函数f（x）=sin（2x+φ）（0＜φ＜π）图象的一条对称轴是x=
，
∴2×
+φ=kπ+
，k∈Z．
∴φ=kπ+
，k∈Z．
又0＜φ＜π，
∴φ=
，
故选：B．
| π |
| 8 |
∴2×
| π |
| 8 |
| π |
| 2 |
∴φ=kπ+
| π |
| 4 |
又0＜φ＜π，
∴φ=
| π |
| 4 |
故选：B．
点评：本题考查函数y=Asin（ωx+φ）的图象与性质，着重考查正弦函数的对称性，得到2×
+φ=kπ+
（k∈Z）是关键，属于中档题．
| π |
| 8 |
| π |
| 2 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图表示甲、乙两名篮球运动员每场得分情况的茎叶图，则甲、乙得分的中位数分别是a，b，则a+b=设z=x+ky，其中x，y满足
，当z的最小值为-
时，k的值为（ ）
|
| 3 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
样本中共有五个个体，其值分别为a，0，1，2，3，若该样本的平均值为1，则样本方差为（ ）
| A、2 | B、2.3 | C、3 | D、3.5 |
“sinα＞0”是“α为锐角”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知双曲线
-
=1的离心率为e，焦点为F的抛物线y2=2px与直线y=k（x-
）交于A，B两点，且
=e，则k的值为（ ）
| x2 |
| 4 |
| y2 |
| 12 |
| p |
| 2 |
| 丨AF丨 |
| 丨BF丨 |
A、2
| ||
B、2
| ||
C、±2
| ||
D、±2
|
将函数y=2sin（
-2x）（x∈[0，π]）向左平移
个单位长度，则平移后函数的单调递增区间是（ ）
| π |
| 3 |
| π |
| 6 |
A、[-
| ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
若实数x、y满足
，则2x-3y的最值情况是（ ）
|
| A、最大值为2，最小值为-4 |
| B、最大值为2，无最小值 |
| C、无最大值，最小值为-4 |
| D、既无最大值，又无最小值 |
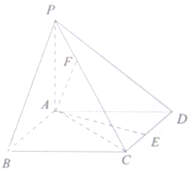如图，已知四棱锥，底面ABCD为菱形，PA⊥平面ABCD，PA=AB=2，∠ABC=60°，E是CD的中点，F为PC上一点，满足FC=2PF．