题目内容
已知函数f(x)=3ex-x2ex-a在R上存在三个零点,则实数a的取值范围为( )
| A、[6e-3,2e] |
| B、(0,2e] |
| C、(-6e-3,0) |
| D、(-6e-3,2e) |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:令f(x)=0,得a=3ex-x2ex,令h(x)=3ex-x2ex,求导数h′(x)=3ex-2xex-x2ex=-ex(x+3)(x-1),由此求出函数f(x)在R上存在3个零点的a的范围.
解答:
解:令f(x)=0,
∴a=3ex-x2ex,
令h(x)=3ex-x2ex,
h′(x)=3ex-2xex-x2ex
=-ex(x+3)(x-1),
∴x<-3时,h′(x)<0,
-3<x<1时,h′(x)>0,
x>1时,h′(x)<0,
∴h(x)min=h(-3)=-6e-3,
h(x)max=h(1)=2e;
∴实数a的取值范围为:(-6e-3,2e),
故选:D.
∴a=3ex-x2ex,
令h(x)=3ex-x2ex,
h′(x)=3ex-2xex-x2ex
=-ex(x+3)(x-1),
∴x<-3时,h′(x)<0,
-3<x<1时,h′(x)>0,
x>1时,h′(x)<0,
∴h(x)min=h(-3)=-6e-3,
h(x)max=h(1)=2e;
∴实数a的取值范围为:(-6e-3,2e),
故选:D.
点评:本题考查函数最值的求法和函数存在3个零点时求a的取值范围.解题时要认真审题,仔细解答,注意导数的应用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
先后掷子(子的六个面上分别标有1,2,3,4,5,6个点)两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x+y为偶数”,事件B为“x,y中有偶数且x≠y”,则概率P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
“sinα>0”是“α为锐角”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
在等差数列{an}中,首项a1=0,公差d≠0,若ap=S9,则p的值为( )
| A、37 | B、20 | C、36 | D、9 |
将函数y=2sin(
-2x)(x∈[0,π])向左平移
个单位长度,则平移后函数的单调递增区间是( )
| π |
| 3 |
| π |
| 6 |
A、[-
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
设a>0,在二项式(a-
)10的展开式中,含x的项的系数与含x4的项的系数相等,则a的值为( )
| x |
| A、1 | B、2 | C、4 | D、8 |
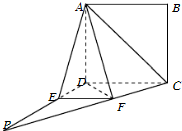 如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.