题目内容
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.(Ⅰ)求证:C1M∥平面A1ADD1;
(Ⅱ)若CD1垂直于平面ABCD且CD1=
| 3 |
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:空间位置关系与距离,空间角,空间向量及应用,立体几何
分析:(Ⅰ)连接AD1,易证AMC1D1为平行四边形,利用线面平行的判定定理即可证得C1M∥平面A1ADD1;
(Ⅱ)作CP⊥AB于P,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间坐标系,易求C1(-1,0,
),D1,(0,0,
),M(
,
,0),
=(1,1,0),
=(
,
,-
),设平面C1D1M的法向量
=(x1,y1,z1),可求得
=(0,2,1),而平面ABCD的法向量
=(1,0,0),从而可求得平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
(Ⅱ)作CP⊥AB于P,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间坐标系,易求C1(-1,0,
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| C1D1 |
| D1M |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| n |
| n1 |
| n2 |
解答:
解:(Ⅰ)连接AD1,∵ABCD-A1B1C1D1为四棱柱,∴CD
C1D1,
又M为AB的中点,∴AM=1.
∴CD∥AM,CD=AM,
∴AM
C1D1,
∴AMC1D1为平行四边形,∴AD1∥MC1,又MC1?平面A1ADD1,AD1?平面A1ADD1,
∴C1M∥平面A1ADD1;
(Ⅱ)解法一:∵AB∥A1B1,A1B1∥C1D1,
∴面D1C1M与ABC1D1共面,
作CN⊥AB,连接D1N,则∠D1NC即为所求二面角,
在ABCD中,DC=1,AB=2,∠DAB=60°,
∴CN=
,
在Rt△D1CN中,CD1=
,CN=
,
∴D1N=
∴cos∠D1CN=
=
=
解法二:作CP⊥AB于P,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间坐标系
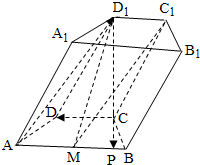
则C1(-1,0,
),D1,(0,0,
),M(
,
,0),
∴
=(1,0,0),
=(-
,
,-
),
设平面C1D1M的法向量
=(x1,y1,z1),
则
,∴
=(0,2,1).
显然平面ABCD的法向量
=(0,0,1),
cos<
,
>|=
=
=
,
显然二面角为锐角,
∴平面C1D1M和平面ABCD所成的角(锐角)的余弦值为
.
| ∥ |
. |
又M为AB的中点,∴AM=1.
∴CD∥AM,CD=AM,
∴AM
| ∥ |
. |
∴AMC1D1为平行四边形,∴AD1∥MC1,又MC1?平面A1ADD1,AD1?平面A1ADD1,
∴C1M∥平面A1ADD1;
(Ⅱ)解法一:∵AB∥A1B1,A1B1∥C1D1,
∴面D1C1M与ABC1D1共面,
作CN⊥AB,连接D1N,则∠D1NC即为所求二面角,
在ABCD中,DC=1,AB=2,∠DAB=60°,
∴CN=
| ||
| 2 |
在Rt△D1CN中,CD1=
| 3 |
| ||
| 2 |
∴D1N=
| ||
| 2 |
∴cos∠D1CN=
| NC |
| D1N |
| ||||
|
| ||
| 5 |
解法二:作CP⊥AB于P,以C为原点,CD为x轴,CP为y轴,CD1为z轴建立空间坐标系

则C1(-1,0,
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴
| C1D1 |
| D1M |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
设平面C1D1M的法向量
| n |
则
|
| n1 |
显然平面ABCD的法向量
| n2 |
cos<
| n1 |
| n2 |
| ||||
|
|
| 1 | ||
|
| ||
| 5 |
显然二面角为锐角,
∴平面C1D1M和平面ABCD所成的角(锐角)的余弦值为
| ||
| 5 |
点评:本题考查用空间向量求平面间的夹角,主要考查空间点、线、面位置关系,二面角等基础知识,同时考查空间想象能力,空间向量的坐标运算,推理论证能力和运算求解能力.

练习册系列答案
相关题目
将函数y=2sin(
-2x)(x∈[0,π])向左平移
个单位长度,则平移后函数的单调递增区间是( )
| π |
| 3 |
| π |
| 6 |
A、[-
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|<
|x-y|.
若对所有x,y∈[0,1],|f(x)-f(y)|<m恒成立,则m的最小值为( )
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|<
| 1 |
| 2 |
若对所有x,y∈[0,1],|f(x)-f(y)|<m恒成立,则m的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线
(θ为参数)的对称中心( )
|
| A、在直线y=2x上 |
| B、在直线y=-2x上 |
| C、在直线y=x-1上 |
| D、在直线y=x+1上 |
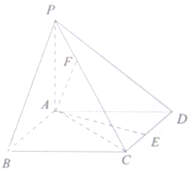 如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.
如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.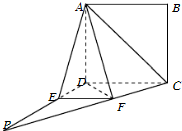 如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E. 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.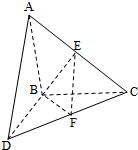 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.