题目内容
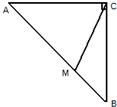
如图，在等腰直角三角形ABC中，在斜边AB上找一点M，则AM＜AC的概率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：几何概型
专题：概率与统计
分析：求出当AM=AC时，对应的长度，利用几何概型的概率公式即可得到结论．
解答：
解：设等腰三角形的两直角边AC=BC=1，则斜边AB=
，
当AM=AC时，AM=1，
∴要使AM＜AC，则AM＜1，
由几何概型的概率公式可知在斜边AB上找一点M，则AM＜AC的概率为
=
，
故选：A．
| 2 |
当AM=AC时，AM=1，
∴要使AM＜AC，则AM＜1，
由几何概型的概率公式可知在斜边AB上找一点M，则AM＜AC的概率为
| 1 | ||
|
| ||
| 2 |
故选：A．
点评：本题主要考查几何概型的概率的计算，根据长度之间的关系是解决本题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
下列结论正确的是（ ）
| A、b⊥c，a⊥b，则a∥c |
| B、a∥α，b⊥α，则a⊥b |
| C、a∥α，b∥α，则a∥b |
| D、a∥α，b?α，则a∥b |
已知双曲线
-
=1的一条渐近线方程为y=
x，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
设A是半径为1的圆周上一定点，P是圆周上一动点，则弦PA＜1的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知菱形ABCD的边长为4，∠ABC=150°，若在菱形内任取一点，则该点到菱形的四个顶点的距离大于1的概率（ ）
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
已知椭圆C：