题目内容
(1)已知x、y都是正实数,求证:x3+y3≥x2y+xy2;
(2)设函数f(x)=|x+1|+|x-5|,x∈R,如果关于x的不等式f(x)≥a-(x-2)2在R上恒成立,求实数a的取值范围.
(2)设函数f(x)=|x+1|+|x-5|,x∈R,如果关于x的不等式f(x)≥a-(x-2)2在R上恒成立,求实数a的取值范围.
考点:函数恒成立问题,不等式的证明
专题:综合题,函数的性质及应用,不等式的解法及应用
分析:(1)用比较法证明不等式,(x3+y3 )-(x2y+xy2)=(x+y)(x-y)2,分析符号可得结论.
(2)转化函数为分段函数求出最小值,然后求出实数a的取值范围.
(2)转化函数为分段函数求出最小值,然后求出实数a的取值范围.
解答:
 证明:(1)∵(x3+y3 )-(x2y+xy2)=x2 (x-y)+y2(y-x)=(x-y)(x2-y2 )
证明:(1)∵(x3+y3 )-(x2y+xy2)=x2 (x-y)+y2(y-x)=(x-y)(x2-y2 )
=(x+y)(x-y)2.
∵x,y都是正实数,∴(x-y)2≥0,(x+y)>0,∴(x+y)(x-y)2≥0,
∴x3+y3≥x2y+xy2.
(2)函数f(x)=|x+1|+|x-5|,x∈R,
关于x的不等式f(x)≥a-(x-2)2,转化为:|x+1|+|x-5|+(x-2)2≥a,在R上恒成立,
令g(x)=|x+1|+|x-5|+(x-2)2=
,
x=2时函数取得最小值为:6,
∴实数a的取值范围:(-∞,6].
 证明:(1)∵(x3+y3 )-(x2y+xy2)=x2 (x-y)+y2(y-x)=(x-y)(x2-y2 )
证明:(1)∵(x3+y3 )-(x2y+xy2)=x2 (x-y)+y2(y-x)=(x-y)(x2-y2 ) =(x+y)(x-y)2.
∵x,y都是正实数,∴(x-y)2≥0,(x+y)>0,∴(x+y)(x-y)2≥0,
∴x3+y3≥x2y+xy2.
(2)函数f(x)=|x+1|+|x-5|,x∈R,
关于x的不等式f(x)≥a-(x-2)2,转化为:|x+1|+|x-5|+(x-2)2≥a,在R上恒成立,
令g(x)=|x+1|+|x-5|+(x-2)2=
|
x=2时函数取得最小值为:6,
∴实数a的取值范围:(-∞,6].
点评:本题考查用比较法证明不等式,基本不等式的应用,将式子变形是证明的关键.函数恒成立问题的应用,考查计算能力以及转化思想.

练习册系列答案
相关题目
从边长为1的正方形的中心和顶点这五点中,随机(等可能)取两点,则该两点间的距离为
的概率是( )
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图可能是下列哪个函数的图象( )


| A、y=2x-x2-1 | ||
B、y=
| ||
| C、y=(x2-2x)ex | ||
D、y=
|
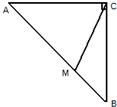
如图,在等腰直角三角形ABC中,在斜边AB上找一点M,则AM<AC的概率为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|