题目内容

若函数y=f（x）的值域是[-2，3]，则函数y=f2（x）的值域是
 
．
考点：函数的值域
专题：函数的性质及应用
分析：采用换元法，令t=f（x），就是求当t∈[-2，3]时，求t2的取值范围．
解答： 解：令t=f（x）∈[-2，3]，则y=f2（x）=t2，∴y∈[0，9]，即函数y=f2（x）的值域是[0，9]．
故答案为：[0，9]．
点评：本题考查的求复合函数的值域，初学者很容易得出值域为[4，9]，而出错．
练习册系列答案
相关题目
如图可能是下列哪个函数的图象（　　）
A、y=2x-x2-1
B、y=
2xsinx
4x+1
C、y=（x2-2x）ex
D、y=
x
lnx
已知曲线f（x）=ax-ex（a＞0）．
（Ⅰ）求曲线在点（0，f（0））处的切线；
（Ⅱ）若存在实数x0使得f（x0）≥0，求a的取值范围．
记max{a，b}为a和b两数中的较大数．设函数f（x）和g（x）的定义域都是R，则“f（x）和g（x）都是偶函数”是“函数F（x）=max{f（x），g（x）}为偶函数”的
 
条件．（在“充分不必要”“必要不充分”“充分必要”和“既不充分也不必要”中选填一个）
函数f（x）=( 
1
4
 )x2-2x的值域为
 
．
函数y=sin(2x-
π
3
)的图象可由函数y=sinx的图象作两次变换得到，第一次变换是针对函数y=sinx的图象而言的，第二次变换是针对第一次变换所得图象而言的．现给出下列四个变换：
A．图象上所有点向右平移
π
6
个单位；
B．图象上所有点向右平移
π
3
个单位；
C．图象上所有点的横坐标变为原来的2倍（纵坐标不变）；
D．图象上所有点的横坐标变为原来的
1
2
倍（纵坐标不变）．
请按顺序写出两次变换的代表字母：
 
．（只要填写一组）
已知O为坐标原点，点M的坐标为（1，-1），点N（x，y）的坐标x，y满足
x+2y-3≤0
x+3y-3≥0
y≤1
，则
OM
•
ON
＜0的概率为
 
．
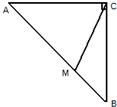
如图，在等腰直角三角形ABC中，在斜边AB上找一点M，则AM＜AC的概率为（　　）
A、
2
2
B、
3
4
C、
2
3
D、
1
2
已知函数f（x）=ax2+lnx（a∈R）
（Ⅰ）当a=2时，求f（x）在区间[e，e2]上的最大值和最小值；
（Ⅱ）如果函数g（x），f1（x），f2（x）在公共定义域D上，满足f1（x）＜g（x）＜f2（x），那么就称g（x）为f1（x），f2（x）的“伴随函数”．已知函数f1(x)=(a-
1
2
)x2+2ax+(1-a2)lnx，f2(x)=
1
2
x2+2ax．若在区间（1，+∞）上，函数f（x）是f1（x），f2（x）的“伴随函数”，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网