题目内容
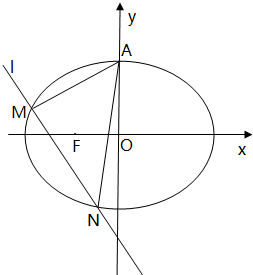已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
（1）求椭圆C的方程；
（2）设直线l交椭圆C于M、N，且F为△AMN的垂心，试求直线l的方程．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）求出直线AF的方程，利用原点O到直线AF的距离为
，求出几何量，即可求椭圆C的方程；
（2）求出l：y=-2x+m代入
+y2=1消y，利用MF⊥AN，可得
•
=0，即（-2-x1，-y1）•（x2，y2-1）=0，从而可得结论．
2
| ||
| 5 |
（2）求出l：y=-2x+m代入
| x2 |
| 5 |
| MF |
| AN |
解答：
解：（1）抛物线y2=-8x的焦点为F（-2，0），
∴直线AF的方程为
+
=1，即bx-2y+2b=0，
∵原点O到直线AF的距离为
，
∴
=
，
∴b=1，
∵c=2，
∴a2=b2+c2=5，
∴椭圆C的方程为
+y2=1；
（2）设l：y=kx+m，
∵KAF=
，且FM⊥l，
∴k=-2，
∴l：y=-2x+m，且设M（x1，y1），N（x2，y2），
由y=-2x+m代入
+y2=1消y，得21x2-20mx+5m2-5=0
△=400m2-84（5m2-5）＞0，x1+x2=
，x1x2=
．
y1y2=（-2x1+m）（-2x2+m）=4x1x2-2m（x1+x2）+m2=
又F为△AMN的垂心，
∴MF⊥AN，∴
•
=0，
∴（-2-x1，-y1）•（x2，y2-1）=0，
∴-2（x1+x2）-x1x2-y1y2+m=0，
∴-2•
-
-
+m=0，
∴6m2+21m-25=0，
∴m=
（正值舍去），
∴直线l的方程为y=-2x+
．
∴直线AF的方程为
| x |
| -2 |
| y |
| b |
∵原点O到直线AF的距离为
2
| ||
| 5 |
∴
| 2b | ||
|
2
| ||
| 5 |
∴b=1，
∵c=2，
∴a2=b2+c2=5，
∴椭圆C的方程为
| x2 |
| 5 |
（2）设l：y=kx+m，
∵KAF=
| 1 |
| 2 |
∴k=-2，
∴l：y=-2x+m，且设M（x1，y1），N（x2，y2），
由y=-2x+m代入
| x2 |
| 5 |
△=400m2-84（5m2-5）＞0，x1+x2=
| 20m |
| 21 |
| 5m2-5 |
| 21 |
y1y2=（-2x1+m）（-2x2+m）=4x1x2-2m（x1+x2）+m2=
| m2-20 |
| 21 |
又F为△AMN的垂心，
∴MF⊥AN，∴
| MF |
| AN |
∴（-2-x1，-y1）•（x2，y2-1）=0，
∴-2（x1+x2）-x1x2-y1y2+m=0，
∴-2•
| 20m |
| 21 |
| 5m2-5 |
| 21 |
| m2-20 |
| 21 |
∴6m2+21m-25=0，
∴m=
-21-
| ||
| 12 |
∴直线l的方程为y=-2x+
-21-
| ||
| 12 |
点评：本题考查椭圆的方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查小时分析解决问题的能力，属于难题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
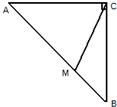
如图，在等腰直角三角形ABC中，在斜边AB上找一点M，则AM＜AC的概率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，F1（-c，0），F2（c，0）分别是双曲线C：