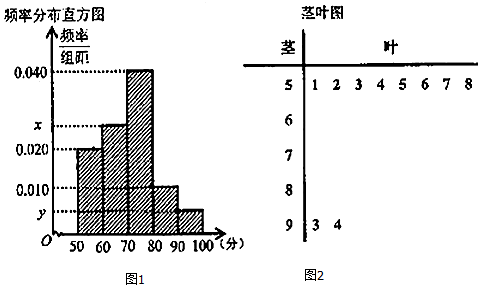
题目内容
2.已知0<α<$\frac{π}{2}$,cos(2π-α)-sin(π-α)=-$\frac{\sqrt{5}}{5}$(1)求sinα+cosα的值;
(2)求sin(2α-$\frac{π}{4}$)的值.
分析 (1)利用诱导公式,同角三角函数的基本关系,求得sinα+cosα的值.
(2)利用求得sinα和cosα的值,再利用两角和差的三角公式、二倍角公式,求得sin(2α-$\frac{π}{4}$)的值.
解答 解:(1)∵已知0<α<$\frac{π}{2}$,cos(2π-α)-sin(π-α)=cosα-sinα=-$\frac{\sqrt{5}}{5}$,
平方可得1-2sinαcosα=$\frac{1}{5}$,∴2sinαcosα=$\frac{4}{5}$,
∴(sinα+cosα)2=1+2sinαcosα=$\frac{9}{5}$,∴sinα+cosα=$\frac{3\sqrt{5}}{5}$.
(2)∵cosα-sinα=-$\frac{\sqrt{5}}{5}$,sinα+cosα=$\frac{3\sqrt{5}}{5}$,
∴sinα=$\frac{2\sqrt{5}}{5}$,cosα=$\frac{\sqrt{5}}{5}$,∴sin2α=2sinαcosα=$\frac{4}{5}$ cos2α=2cos2α-1=-$\frac{3}{5}$,
∴sin2αcos$\frac{π}{4}$-cos2αsin$\frac{π}{4}$=$\frac{2\sqrt{5}}{5}•\frac{\sqrt{2}}{2}$-(-$\frac{3}{5}$)•$\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的三角公式、二倍角公式、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
12.《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织得快,而且每天增加的数量相同,已知第一天织布10尺,一个月(按30天计算)总共织布6尺,问每天增加的数量为多少尺?该问题的答案为( )
| A. | $\frac{8}{29}$尺 | B. | $\frac{16}{29}$尺 | C. | $\frac{32}{29}$尺 | D. | $\frac{1}{2}$尺 |
12.已知直线mx+4y-2=0与2x-5y+1=0互相垂直,则m的值为( )
| A. | 10 | B. | 20 | C. | 0 | D. | -4 |
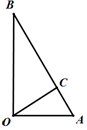 根据平面向量基本定理,若$\overrightarrow{e_1},\overrightarrow{e_2}$为一组基底,同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则向量$\overrightarrow a$与有序实数对(x,y)一一对应,称(x,y)为向量$\overrightarrow a$在基底$\overrightarrow{e_1},\overrightarrow{e_2}$下的坐标;特别地,若$\overrightarrow{e_1},\overrightarrow{e_2}$分别为x,y轴正方向的单位向量$\overrightarrow i,\overrightarrow j$,则称(x,y)为向量$\overrightarrow a$的直角坐标.
根据平面向量基本定理,若$\overrightarrow{e_1},\overrightarrow{e_2}$为一组基底,同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则向量$\overrightarrow a$与有序实数对(x,y)一一对应,称(x,y)为向量$\overrightarrow a$在基底$\overrightarrow{e_1},\overrightarrow{e_2}$下的坐标;特别地,若$\overrightarrow{e_1},\overrightarrow{e_2}$分别为x,y轴正方向的单位向量$\overrightarrow i,\overrightarrow j$,则称(x,y)为向量$\overrightarrow a$的直角坐标.