题目内容
17．一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则P（B|A）是$\frac{4}{7}$．分析 根据题意，利用条件概率计算公式求出事件A发生的条件下事件B发生的概率即可．
解答 解：一个口袋中装有5个白球，3个红球，每次从袋中随机摸出一个球，不放回地摸2次，
A表示“第一次拿出的是白球”，B表示“第二次拿出的是白球”，
则P（A）=$\frac{5}{8}$，P（AB）=$\frac{5}{8}×\frac{4}{7}$=$\frac{5}{14}$；
在摸出的第一个是白球的条件下，摸出的第二个球是白球的概率是：
p（B|A）=$\frac{\frac{5}{14}}{\frac{5}{8}}$=$\frac{4}{7}$．
故答案为$\frac{4}{7}$．
点评 本题考查了条件概率的计算问题，是基础题目．
练习册系列答案
相关题目
7．
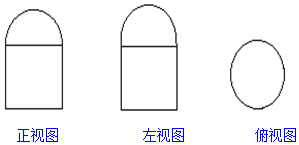如图所示，是一个组合体的三视图，图中四边形是边长为2的正方形，圆的直径为2，那么这个组合体的表面积是（ ）
如图所示，是一个组合体的三视图，图中四边形是边长为2的正方形，圆的直径为2，那么这个组合体的表面积是（ ）| A． | 5π | B． | 6π | C． | 7π | D． | 8π |
8．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（ ）
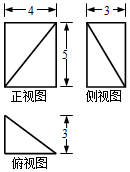
| A． | 10cm3 | B． | 20cm3 | C． | 30cm3 | D． | 40cm3 |
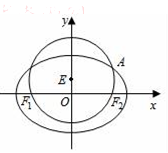已知圆E：x2+（y-$\frac{1}{2}$）2=$\frac{9}{4}$，经过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点F1，F2，且与椭圆C在第一象限的交点为A，且F1，E，A三点共线，直线l交椭圆C于M，N两点，且与直线OA平行．
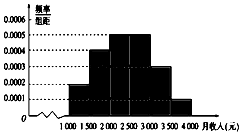某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．
6．设m、n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题，其中正确命题的序号是（ ）
①若m⊥α，n⊥α，则m⊥n；
②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m∥α，n∥α，则m∥n；
④若α⊥γ，β⊥γ，则α⊥β．
①若m⊥α，n⊥α，则m⊥n；
②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m∥α，n∥α，则m∥n；
④若α⊥γ，β⊥γ，则α⊥β．
| A． | ② | B． | ②③ | C． | ③④ | D． | ①④ |
7．在区间$[{-\frac{π}{4}，\frac{2π}{3}}]$上任取一个数x，则函数f（x）=3sin2x的值不小于0的概率为（ ）
| A． | $\frac{6}{11}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{7}{12}$ |