题目内容

14．在平面直角坐标系xOy中，曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8．

分析 x＞0，y＞0时，方程化为（x-1）2+（y-1）2=2，其面积为$\frac{3}{4}•π•2+2$=$\frac{3π}{2}$+2，根据图象的对称性，可得曲线x2+y2=2|x|+2|y|围成的图形的面积．

解答 解：x＞0，y＞0时，方程化为（x-1）2+（y-1）2=2，其面积为$\frac{3}{4}•π•2+2$=$\frac{3π}{2}$+2
根据图象的对称性，可得曲线x2+y2=2|x|+2|y|围成的图形的面积为6π+8，
故答案为6π+8．

点评 本题考查曲线方程，考查面积的计算，正确化简曲线是关键．

练习册系列答案
相关题目
4．在单调递增的等差数列{an}中，a3，a7，a15成等比数列，前5项之和等于20．
（1）求数列{an}的通项公式；
（2）设${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$，记数列{bn}的前n项和为Tn，求使${T_n}≤\frac{24}{25}$成立的n的最大值．
5．已知椭圆$C：\frac{x^2}{16}+\frac{y^2}{7}=1$，F为椭圆的右焦点，B为椭圆的上顶点，P是椭圆上一动点．
（1）求|OP|2+|PF|2的取值范围
（2）已知直线l：x+y=1，点P到直线l的距离为d，求d的取值范围．
2．已知0＜α＜$\frac{π}{2}$，cos（2π-α）-sin（π-α）=-$\frac{\sqrt{5}}{5}$
（1）求sinα+cosα的值；
（2）求sin（2α-$\frac{π}{4}$）的值．
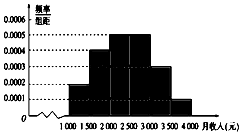9．某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．
（1）求居民收入在[3000，3500）的频率；
（2）根据频率分布直方图算出样本数据的中位数、平均数及其众数；
（3）为了分析居民的收入与年龄、职业等方面的关系，按收入从这10000人中用分层抽样方法抽出100人作进一步分析，则应在月收入为[2500，3000）的人中抽取多少人？
19．已知函数$f（x）=x+\frac{a}{x}-2lnx$．
（1）当a=0时，求f（x）在点（1，f（1））处的切线方程；
（2）是否存在实数a，当0＜x≤2时，函数f（x）图象上的点都在$\left\{\begin{array}{l}0＜x≤2\\ x-y≥0\end{array}\right.$所表示的平面区域（含边界）？若存在，求出a的值组成的集合；否则说明理由；
（3）若f（x）有两个不同的极值点m，n（m＞n），求过两点M（m，f（m）），N（n，f（n））的直线的斜率的取值范围．
6．设m、n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题，其中正确命题的序号是（　　）
①若m⊥α，n⊥α，则m⊥n；
②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m∥α，n∥α，则m∥n；
④若α⊥γ，β⊥γ，则α⊥β．
A．②B．②③C．③④D．①④
3．已知命题p：不等式x2-ax-8＞0对任意实数x∈[2，4]恒成立；命题q：存在实数θ满足$\frac{4}{a-1}≤sinθ-2$；命题r：不等式ax2+2x-1＞0有解．
（1）若p∧q为真命题，求a的取值范围．
（2）若命题p、q、r恰有两个是真命题，求实数a的取值范围．
4．古式楼阁中的横梁多为木质长方体结构，当横梁的长度一定时，其强度与宽成正比，与高的平方成正比．现将一圆柱形木头锯成一横梁（长度不变），当高与宽的比值为$\sqrt{2}$时，横梁的强度最大．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网