题目内容
12．已知直线mx+4y-2=0与2x-5y+1=0互相垂直，则m的值为（ ）| A． | 10 | B． | 20 | C． | 0 | D． | -4 |
分析 由直线的垂直关系可得2m-20=0，解方程可得m的值．
解答 解：∵直线mx+4y-2=0与2x-5y+1=0垂直，
∴2m-20=0，解得m=10，
故选：A
点评 本题考查直线的一般式方程和垂直关系，属基础题．
练习册系列答案
相关题目
7．在区间$[{-\frac{π}{4}，\frac{2π}{3}}]$上任取一个数x，则函数f（x）=3sin2x的值不小于0的概率为（ ）
| A． | $\frac{6}{11}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{7}{12}$ |
17．如图在空间四边形OABC中，点M在OA上，且OM=2MA，N为BC中点，则$\overrightarrow{MN}$等于（ ）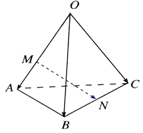
| A． | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B． | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C． | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D． | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
2．
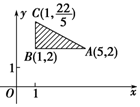如图所示的坐标平面的可行域内（包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（ ）
如图所示的坐标平面的可行域内（包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{3}{5}$ | C． | 4 | D． | $\frac{5}{3}$ |