题目内容
7.若直线x+y+m=0上存在点P可作圆O:x2+y2=1的两条切线PA、PB,切点为A、B,且∠APB=60°,则实数m的取值范围为$[-2\sqrt{2},2\sqrt{2}]$.分析 当PO和直线x+y+m=0垂直时,∠APB的最大值为60°,此时∠APO=30°,PO=2r=2,从而圆心O到直线x+y+m=0的距离小于等于2,再利用点到直线的距离公式求得实数m的取值范围.
解答 解:由题意可得,当PO和直线x+y+m=0垂直时,∠APB的最大值为60°,此时∠APO=30°,PO=2r=2,
则圆心O到直线x+y+m=0的距离小于等于2,即$\frac{|m|}{\sqrt{2}}$≤2,解得m∈$[-2\sqrt{2},2\sqrt{2}]$,
故答案为$[-2\sqrt{2},2\sqrt{2}]$.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
15.函数y=Asin(ωx+ϕ)$(ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则函数表达式为( )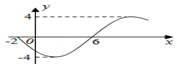

| A. | $y=-4sin(\frac{π}{8}x-\frac{π}{4})$ | B. | $y=4sin(\frac{π}{8}x-\frac{π}{4})$ | C. | $y=-4sin(\frac{π}{8}x+\frac{π}{4})$ | D. | $y=4sin(\frac{π}{8}x+\frac{π}{4})$ |
17.如图在空间四边形OABC中,点M在OA上,且OM=2MA,N为BC中点,则$\overrightarrow{MN}$等于( )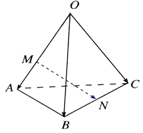

| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
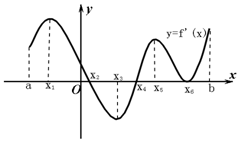 如图是导函数y=f′(x)的图象,对于函数y=f(x)的极值点的说法:?
如图是导函数y=f′(x)的图象,对于函数y=f(x)的极值点的说法:?