Question

11．一次测试中，为了了解学生的学习情况，从中抽取了n个学生的成绩进行统计．按照的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出得分在的数据）．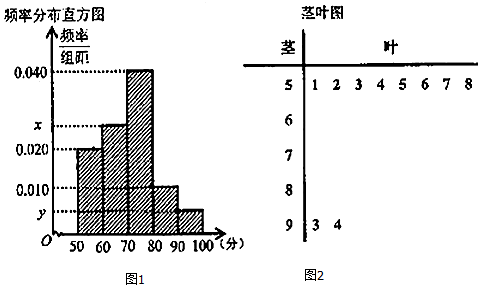

（1）求样本容量n和频率分布直方图中x，y的值；
（2）求这n名同学成绩的平均数、中位数及众数；
（3）在选取的样本中，从成绩是80分以上（含80分）的同学中随机抽取3名同学参加志愿者活动，求这3名同学中恰有两名同学得分在[90，100]内的概率．

Answer 1

分析 （1）利用频率分布直方图，结合频率=$\frac{频数}{总数}$，能求出样本容量n和频率分布直方图中x、y的值．
（2）由频率分布直方图能求出这n名同学成绩的平均数、中位数及众数．
（3）由题意，分数在[80，90）内的有4人，分数在[90，100]内的有2人，成绩是80分以上（含80分）的学生共6人．从成绩是80分以上（含80分）的同学中随机抽取3名同学参加志愿者活动，利用等可能事件概率计算公式能求出这3名同学中恰有两名同学得分在[90，100]内的概率．

解答 解：（1）由题意可知，样本容量n=$\frac{8}{0.02×10}$=40，
y=$\frac{2}{40}$÷10=0.005，
x=$\frac{1-（0.002+0.004+0.01+0.005）×10}{10}$=0.025．
（2）由频率分布直方图得：
这n名同学成绩的平均数：
$\overline{x}$=0.020×10×55+0.025×10×65+0.040×10×75+0.010×10×85+0.005×10×95=70.5，
∵成绩在[50，70）的频率为（0.020+0.025）×10=0.45，
成绩在[70，80）的频率为0.040×10=0.4，
∴中位数为：70+$\frac{0.5-0.45}{0.4}×10$=71.25，
众数为：$\frac{70+80}{2}$=75．
（3）由题意，分数在[80，90）内的有：0.01×10×40=4人，
分数在[90，100]内的有：0.005×10×40=2人，
∴成绩是80分以上（含80分）的学生共6人．
从成绩是80分以上（含80分）的同学中随机抽取3名同学参加志愿者活动，
基本事件总数N=${C}_{6}^{3}$=20，
这3名同学中恰有两名同学得分在[90，100]内包含的基本事件个数M=${C}_{2}^{2}{C}_{4}^{1}$=4，
∴这3名同学中恰有两名同学得分在[90，100]内的概率p=$\frac{M}{N}$=$\frac{4}{20}=\frac{1}{5}$．

点评 本题考查频率分布直方图的应用，考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．