题目内容
（几何证明选讲） 如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=3，AC=3| 3 |
| 5 |
考点：与圆有关的比例线段
专题：立体几何
分析：利用切割线定理可得AD2=AB•AC，解得AB．进而得到BC．过圆心O作OE⊥BC，垂足为点E．利用垂径定理可得：CE=EB=
BC．在Rt△OCE中，利用勾股定理可得OE=
即可得出．
| 1 |
| 2 |
| OC2-CE2 |
解答：
解：由从圆O外一点A引圆的切线AD和割线ABC，利用切割线定理可得AD2=AB•AC，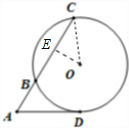
∴AB=
=
=
．
∴BC=AC-BC=2
．
过圆心O作OE⊥BC，垂足为点E．
则CE=EB=
．
在Rt△OCE中，OE=
=
=
．
故答案为：
．
∴AB=
| AD2 |
| AC |
| 32 | ||
3
|
| 3 |
∴BC=AC-BC=2
| 3 |
过圆心O作OE⊥BC，垂足为点E．
则CE=EB=
| 3 |
在Rt△OCE中，OE=
| OC2-CE2 |
(
|
| 2 |
故答案为：
| 2 |
点评：本题考查了圆的切割线定理、垂径定理和勾股定理，属于基础题．
练习册系列答案
相关题目
