题目内容
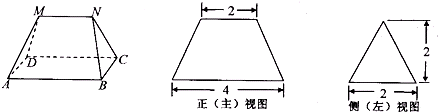
多面体MN-ABCD的底面ABCD为矩形，其正视图和侧视图如图，其中正视图为等腰梯形，侧视图为等腰三角形，则该多面体的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：将多面体补成一个侧棱长为4的直三棱柱，结合图形判断直三棱柱的底面三角形及相关几何量的数据，判断补的两个三棱锥的高，把数据代入棱柱与棱锥的体积公式计算．
解答：
解：将多面体补成一个侧棱长为4的直三棱柱，如图，
则直三棱柱的底面三角形如左视图所示，一条边长为2．该边上的高为2，
补的两个三棱锥的高都是1，
∴几何体的体积V=
×2×2×4-2×
×
×2×2×1=8-
=
．
故选：D．
则直三棱柱的底面三角形如左视图所示，一条边长为2．该边上的高为2，
补的两个三棱锥的高都是1，
∴几何体的体积V=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 20 |
| 3 |
故选：D．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知两点A（1，0），B（b，0），若抛物线y2=4x上存在点C使△ABC为等边三角形，则b=（ ）
| A、5 | ||
B、5或-
| ||
| C、4 | ||
| D、4或-2 |
已知定义在R上的函数f（x）、g（x）满足
=ax，且f′（x）g（x）＜f（x）g′（x），
+
=
，若有穷数列{
}（n∈N*）的前n项和为
，则n=（ ）
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| 127 |
| 128 |
| A、4 | B、5 | C、6 | D、7 |
已知全集为R，集合A={-1，0，1}，B={x|（
）x≤1}，则A∩∁RB等于（ ）
| 1 |
| 2 |
| A、（-∞，0） |
| B、[0，+∞） |
| C、{-1} |
| D、{0，1} |
设变量x，y满足约束条件
，则z=2x-y的最大值为（ ）
|
| A、-3 | ||
B、
| ||
| C、5 | ||
| D、6 |
过点P（4，2）作圆x2+y2=4的两条切线，切点分别为A、B，O为坐标原点，则△PAB的外接圆方程是（ ）
| A、（x-2）2+（y-1）2=5 |
| B、（x-4）2+（y-2）2=20 |
| C、（x+2）2+（y+1）2=5 |
| D、（x+4）2+（y+2）2=20 |