题目内容
已知函数f(x)=1nx+x-
(a≥-2),g(x)=ex-x,其中e为自然对数的底数,且当x>0时f(x)≥3恒成立.
(Ⅰ)求g(x)的单调区间;
(Ⅱ)求实数a的所有可能取值的集合;
(Ⅲ)求证:f(x)+g(x)>4.
| a |
| x |
(Ⅰ)求g(x)的单调区间;
(Ⅱ)求实数a的所有可能取值的集合;
(Ⅲ)求证:f(x)+g(x)>4.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)确定定义域,求g'(x),由 g'(x)>0求得增区间,由 g'(x)<0求得减区间;
(Ⅱ)利用在区间D上,a≤f(x)恒成立,则a≤f(x)min求解;
(Ⅲ)利用构造法,构造新函数求解.
(Ⅱ)利用在区间D上,a≤f(x)恒成立,则a≤f(x)min求解;
(Ⅲ)利用构造法,构造新函数求解.
解答:
解:(Ⅰ)g'(x)=ex-1,g'(x)<0⇒x<0,g'(x)>0⇒x>0,
∴g(x)的减区间是(-∞,0),增区间是(0,+∞).
(Ⅱ)f(x)=lnx+x-
≥3恒成立,即
≤lnx+x-3,
∵x>0,∴a≤xlnx+x2-3x恒成立.
设h(x)=xlnx+x2-3x,(x>0),h'(x)=lnx+2x-2,
由于h'(x)在(0,+∞)上是增函数,且h'(1)=0,
∴x∈(0,1)时,h'(x)<0,h(x)是减函数,x∈(1,+∞)时,h'(x)>0,h(x)是增函数,
∴h(x)min=h(1)=-2,从而若a≤xlnx+x2-3x恒成立,必有a≤-2.
又∵a≥-2,
∴a的取值集合为{-2}.
(Ⅲ)由(Ⅰ)知,g(x)≥g(0)=1,即ex-x≥1,当且仅当x=0时等号成立,
∴x>0时,有ex>x+1.
∴f(x)+g(x)=lnx+ex+
>lnx+x+1+
,
设F(x)=lnx+x+1+
(x>0),
则F′(x)=
+1-
=
=
,
当x∈(0,1)时,F'(x)<0,F(x)是减函数,
当x∈(1,+∞)时,F'(x)>0,F(x)是增函数,
∴F(x)≥F(1)=4,
即f(x)+g(x)>4成立.
∴g(x)的减区间是(-∞,0),增区间是(0,+∞).
(Ⅱ)f(x)=lnx+x-
| a |
| x |
| a |
| x |
∵x>0,∴a≤xlnx+x2-3x恒成立.
设h(x)=xlnx+x2-3x,(x>0),h'(x)=lnx+2x-2,
由于h'(x)在(0,+∞)上是增函数,且h'(1)=0,
∴x∈(0,1)时,h'(x)<0,h(x)是减函数,x∈(1,+∞)时,h'(x)>0,h(x)是增函数,
∴h(x)min=h(1)=-2,从而若a≤xlnx+x2-3x恒成立,必有a≤-2.
又∵a≥-2,
∴a的取值集合为{-2}.
(Ⅲ)由(Ⅰ)知,g(x)≥g(0)=1,即ex-x≥1,当且仅当x=0时等号成立,
∴x>0时,有ex>x+1.
∴f(x)+g(x)=lnx+ex+
| 2 |
| x |
| 2 |
| x |
设F(x)=lnx+x+1+
| 2 |
| x |
则F′(x)=
| 1 |
| x |
| 2 |
| x2 |
| x2+x-2 |
| x2 |
| (x+2)(x-1) |
| x2 |
当x∈(0,1)时,F'(x)<0,F(x)是减函数,
当x∈(1,+∞)时,F'(x)>0,F(x)是增函数,
∴F(x)≥F(1)=4,
即f(x)+g(x)>4成立.
点评:本题主要考查利用导数法判断函数的单调性求函数的最值等问题,考查恒成立问题的转化能力及构造函数法解决问题的能力,属难题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
复数z=|(
-i)i|+i5(i为虚数单位),则复数z的共轭复数为( )
| 3 |
| A、2-i | B、2+i |
| C、4-i | D、4+i |
已知向量
=(2,-1),
(x,4),且
⊥
,则|
+
|的值为( )
| p |
| q |
| p |
| q |
| p |
| q |
A、
| ||
| B、5 | ||
C、
| ||
| D、13 |
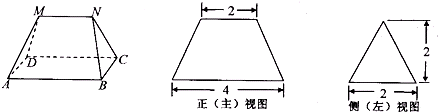
多面体MN-ABCD的底面ABCD为矩形,其正视图和侧视图如图,其中正视图为等腰梯形,侧视图为等腰三角形,则该多面体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.
某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.