题目内容
过点P（4，2）作圆x2+y2=4的两条切线，切点分别为A、B，O为坐标原点，则△PAB的外接圆方程是（ ）
| A、（x-2）2+（y-1）2=5 |
| B、（x-4）2+（y-2）2=20 |
| C、（x+2）2+（y+1）2=5 |
| D、（x+4）2+（y+2）2=20 |
考点：圆的切线方程
专题：直线与圆
分析：根据已知圆的方程找出圆心坐标，发现圆心为坐标原点，根据题意可知，△ABP的外接圆即为四边形OAPB的外接圆，从而得到线段OP为外接圆的直径，其中点为外接圆的圆心，根据P和O两点的坐标利用两点间的距离公式求出|OP|的长即为外接圆的直径，除以2求出半径，利用中点坐标公式求出线段OP的中点即为外接圆的圆心，根据求出的圆心坐标和半径写出外接圆的方程即可．
解答：
解：由圆x2+y2=4，得到圆心O坐标为（0，0），
∴△ABP的外接圆为四边形OAPB的外接圆，又P（4，2），
∴外接圆的直径为|OP|=
=2
，半径为
，
外接圆的圆心为线段OP的中点是（
，
），即（2，1），
则△ABP的外接圆方程是（x-2）2+（y-1）2=5．
故选：A．
∴△ABP的外接圆为四边形OAPB的外接圆，又P（4，2），
∴外接圆的直径为|OP|=
| 42+22 |
| 5 |
| 5 |
外接圆的圆心为线段OP的中点是（
| 4+0 |
| 2 |
| 2+0 |
| 2 |
则△ABP的外接圆方程是（x-2）2+（y-1）2=5．
故选：A．
点评：本题考查了直线与圆的位置关系，要求学生熟练运用两点间的距离公式及中点坐标公式．根据题意得到△ABP的外接圆为四边形OAPB的外接圆是本题的突破点．
练习册系列答案
相关题目
已知集合M={x|x2-px+6=0}，N={x|x2+6x-q=0}，若M∩N={2}，则p+q的值为（ ）
| A、21 | B、8 | C、7 | D、6 |
已知集合A={x|x（3-x）＞0}，集合B={y|y=2x+2}，则A∩B=（ ）
| A、{x|2＜x＜3} |
| B、{x|x＜0或x＞2} |
| C、{x|x＞3} |
| D、{x|x＜0或x≥2} |
若不等式组
表示的平面区域内存在点M（x0，y0），满足2x0+y0=6，则实数m的取值范围是（ ）
|
| A、[1，+∞） |
| B、[0，1] |
| C、（0，1） |
| D、[0，2] |
多面体MN-ABCD的底面ABCD为矩形，其正视图和侧视图如图，其中正视图为等腰梯形，侧视图为等腰三角形，则该多面体的体积是（ ）
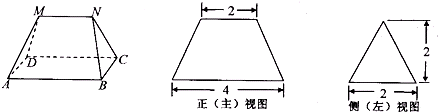
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|-2＜x≤1}，B={x|2x≤1}，则A∩B等于（ ）
| A、{x|-2＜x≤-1} |
| B、{x|-2＜x≤1} |
| C、{x|-2＜x≤0} |
| D、{x|-1＜x≤0} |
某校在一次期末数学统测中，为统计学生的考试情况，从学校的2000名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于60分到140分之间（满分150分），将统计结果按如下方式分成八组：第一组[60，70），第二组[70，80），…，第八组[130，140]，如图是按上述分组方法得到的频率分布直方图的一部分．