题目内容
已知函数f(x)=ax-ex(a∈R).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设g(x)=x2-2x+1,证明:当1<a<e时,对任意x1∈(-∞,+∞),总存在x2∈[0,1],使得f(x1)<g(x2)成立.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设g(x)=x2-2x+1,证明:当1<a<e时,对任意x1∈(-∞,+∞),总存在x2∈[0,1],使得f(x1)<g(x2)成立.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,分类讨论,利用导数的正负,可求f(x)的单调区间;
(Ⅱ)由已知,转化为f(x)max<g(x)max,求最值可证.
(Ⅱ)由已知,转化为f(x)max<g(x)max,求最值可证.
解答:
解:(Ⅰ)f'(x)=a-ex,
当a≤0时,f'(x)<0,所以,f(x)在(-∞,+∞)上单调递减,
当a>0时,由f'(x)=0,得x=lna.
在区间(-∞,lna)上,f'(x)>0,在区间(lna,+∞)上f'(x)<0
所以,函数f(x)的单调递增区为(-∞,lna),单调递减区间为(lna,+∞)
所以,当a≤0时,f(x)在(-∞,+∞)上单调递减,
当a>0时,函数f(x)的单调递增区间为(-∞,lna),单调递减区间为(lna,+∞)
(Ⅱ)证明:由已知,转化为f(x)max<g(x)max,由已知可知g(x)max=g(0)=1,
当1<a<e时,f(x)在(-∞,lna)上单调递增,在(lna,+∞)上单调递减,
故f(x)的极大值即为最大值,f(lna)=alna-a,
而1<a<e,故f(lna)=alna-a=a(lna-1)<0,
所以1>alna-a,故命题成立.
当a≤0时,f'(x)<0,所以,f(x)在(-∞,+∞)上单调递减,
当a>0时,由f'(x)=0,得x=lna.
在区间(-∞,lna)上,f'(x)>0,在区间(lna,+∞)上f'(x)<0
所以,函数f(x)的单调递增区为(-∞,lna),单调递减区间为(lna,+∞)
所以,当a≤0时,f(x)在(-∞,+∞)上单调递减,
当a>0时,函数f(x)的单调递增区间为(-∞,lna),单调递减区间为(lna,+∞)
(Ⅱ)证明:由已知,转化为f(x)max<g(x)max,由已知可知g(x)max=g(0)=1,
当1<a<e时,f(x)在(-∞,lna)上单调递增,在(lna,+∞)上单调递减,
故f(x)的极大值即为最大值,f(lna)=alna-a,
而1<a<e,故f(lna)=alna-a=a(lna-1)<0,
所以1>alna-a,故命题成立.
点评:本题考查导数知识的综合运用,考查函数的单调性与最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
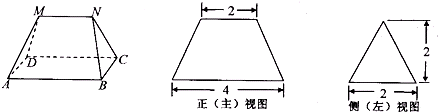
多面体MN-ABCD的底面ABCD为矩形,其正视图和侧视图如图,其中正视图为等腰梯形,侧视图为等腰三角形,则该多面体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.
某校在一次期末数学统测中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140],如图是按上述分组方法得到的频率分布直方图的一部分. 
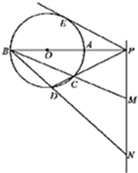 如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.
如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.