题目内容
已知定义在R上的函数f(x)、g(x)满足
=ax,且f′(x)g(x)<f(x)g′(x),
+
=
,若有穷数列{
}(n∈N*)的前n项和为
,则n=( )
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| 127 |
| 128 |
| A、4 | B、5 | C、6 | D、7 |
考点:导数的运算,利用导数研究函数的单调性
专题:导数的概念及应用
分析:根据函数的单调性和导数之间的关系,求出a的取值范围,再由
+
=
,即可得到a的值,然后利用等比数列的前n项和公式即可得到结论.
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
解答:
解:由于[
]′=
<0,
故函数
=ax单调递减,所以0<a<1.
又
+
=
,即a+a-1=
,解得a=
或a=2(舍).
所以
=(
)x,
故{
}(n∈N*)是首项为
=
,公比q=
,
所以前n项和为
=1-(
)n,
由1-(
)n=
得n=7.
故选:D.
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
故函数
| f(x) |
| g(x) |
又
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
所以
| f(x) |
| g(x) |
| 1 |
| 2 |
故{
| f(n) |
| g(n) |
| f(1) |
| g(1) |
| 1 |
| 2 |
| 1 |
| 2 |
所以前n项和为
| ||||
1-
|
| 1 |
| 2 |
由1-(
| 1 |
| 2 |
| 127 |
| 128 |
故选:D.
点评:本题主要考查函数单调性和导数之间的关系,等比数列的前n项和公式的计算,考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数z=|(
-i)i|+i5(i为虚数单位),则复数z的共轭复数为( )
| 3 |
| A、2-i | B、2+i |
| C、4-i | D、4+i |
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知满足约束条件
的可行域为Ω,直线x+ky-1=0将可行域Ω划分成面积相等的两部分,则k的值为( )
|
A、-
| ||
B、
| ||
| C、0 | ||
D、
|
已知集合A={x|x(3-x)>0},集合B={y|y=2x+2},则A∩B=( )
| A、{x|2<x<3} |
| B、{x|x<0或x>2} |
| C、{x|x>3} |
| D、{x|x<0或x≥2} |
已知向量
=(2,-1),
(x,4),且
⊥
,则|
+
|的值为( )
| p |
| q |
| p |
| q |
| p |
| q |
A、
| ||
| B、5 | ||
C、
| ||
| D、13 |
多面体MN-ABCD的底面ABCD为矩形,其正视图和侧视图如图,其中正视图为等腰梯形,侧视图为等腰三角形,则该多面体的体积是( )
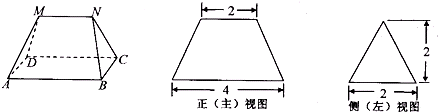

A、
| ||||
B、
| ||||
C、
| ||||
D、
|